Аннотация проекта
Развитие современных представлений о физических свойствах материи и пространства-времени в космологических масштабах приводит к необходимости прецизионных измерений, таких как измерение анизотропии и поляризации реликтового излучения, детектирование гравитационных волн, уточнение значения параметра Хаббла в современную эпоху повторного расширения вселенной и многих других экспериментов.
Для описания физических процессов, происходящих в ранней Вселенной, в настоящее время, используются теоретические модели космологической инфляции на основе теории гравитации Эйнштейна и ее модификаций. Данные модели подразумевают существование стадии ускоренного расширения, предшествующей стадии горячей Вселенной. В качестве материальной компоненты, определяющей динамику ускоренного расширения, как правило, рассматривается некоторое экзотическое вещество с отрицательным давлением, в простейшем случае - каноническое скалярное поле. Модели космологической инфляции позволяют решить многие проблемы, возникающие в теории Большого Взрыва, например, проблемы однородности и изотропии, плоскостности, горизонта, первичных монополей и некоторые другие проблемы. Также первичные неоднородности, на основе которых сформировалась наблюдаемая крупномасштабная структура Вселенной, могли быть сгенерированы во время стадии космологической инфляции как следствие квантовых флуктуаций скалярного поля и соответствующих возмущений метрики пространства-времени.
В настоящее время, в контексте инфляционной парадигмы, рассматривается большое число космологических моделей, основанных на эволюции различных типов скалярных полей в рамках теории гравитации Эйнштейна. Важным направлением развития представлений о физических процессах, происходящих в ранней вселенной, является учет различных поправок к общей теории относительности, которые проявляются в модификации действия Эйнштейна-Гильберта. Также, модифицированные теории гравитации позволяют разрешить проблему темной энергии, то есть дают объяснение повторного ускоренного расширения вселенной без необходимости привлечения экзотических видов материи.
Важным следствием инфляционных моделей ранней вселенной является существование реликтовых гравитационных волн, оценка влияния которых на анизотропию и поляризацию реликтового излучения составляет основу экспериментальной проверки инфляционных сценариев эволюции ранней Вселенной. Следует отметить, что реликтовые гравитационные волны не были зарегистрированы непосредственно, и решение проблемы их детектирования представляет собой одну из важных задач современной физики.
Для успешного решения данной задачи важное значение имеет теоретическое описание спектров гравитационно-волновых возмущений в моделях ранней вселенной, соответствующих современным наблюдательным ограничениям.
Таким образом, основной задачей данного проекта является построение феноменологически корректных моделей космологической инфляции на основе гравитации Эйнштейна и ее модификаций, подразумевающих точную оценку характеристик реликтовых гравитационных волн, таких как диапазон частот, в котором их плотность энергии максимальна, что можно использовать в работе существующих и проектировании перспективных детекторов реликтовых гравитационных волн.

Цели и задачи проекта

Определить условия обнаружения реликтовых (первичных) гравитационных волн по их вкладу во флуктуации фонового микроволнового излучения и анализу В-компоненты его поляризации на основе селекции моделей модифицированной космологии.

Для достижения поставленной цели планируется построение новых космологических моделей на основе модифицированных теорий гравитации, параметры которых согласованы с как наблюдательными данным миссий WMAP, PLANCK и BICEP2 так и с ограничениями, основанными на непосредственном детектировании гравитационных волн от слияния нейтронных звезд и черных дыр в проектах LIGO и VIRGO. Анализ расхождения скалярно-тензорного отношения по данным этих миссий на основе точнорешаемых моделей с приближением медленного скатывания.
Сопоставление фоновой динамики и параметров космологических возмущений для рассматриваемых моделей со стандартными моделями космологической инфляции. Теоретический анализ характеристик реликтовых гравитационных волн в построенных моделях ранней вселенной.

Конкретная программа связана с решением следующих задач:
1) Разработка новых методов приближенного и точного анализа космологических
моделей на ранней (инфляционной) стадии эволюции Вселенной.
2) Оценка расхождения между точными и приближенными решениями на уровне
космологической динамики и уточнение спектральных параметров космологических возмущений по сравнению с полученными из приближения медленного скатывания.
3) Поиск новых методов верификации космологических моделей на основе модификации их параметров в рамках ОТО и анализа влияния неминимального взаимодействия скалярного поля и кривизны для случая модифицированных теорий гравитации.
4) Поиск функциональных и параметрических связей между космологическими моделями, основанными на ОТО и модифицированных теориях гравитации в четырехмерном пространстве Фридмана-Робертсона-Уокера.
5) Качественная и количественная оценка влияния модификаций гравитации Эйнштейна на параметры космологических моделей. Поиск моделей, построенных на основе модификаций ОТО с эквивалентными случаю гравитации Эйнштейна параметрами.
6) Развитие методов построения точных решений, обобщенных на случай различных теорий гравитации и двух стадий ускоренного расширения Вселенной с возможностью их редукции к частным случаям.
 

Основные публикации по проекту за 2020 год

1. K. A. Bolshakova1 and S. V. Chervon. Cosmological Solutions in the Tensor-Multi-Scalar Theory of Gravity with the Higgs Potential. Gravitation and Cosmology, 2020, Vol. 26, No. 2, pp. 153–161. c

2. Червон С. В., Фабрис Ж.С., Фомин И. В. СФЕРИЧЕСКИ-СИММЕТРИЧНЫЕ РЕШЕНИЯ В F(R) ГРАВИТАЦИИ С КИНЕТИЧЕСКИМ СКАЛЯРОМ КРИВИЗНЫ. ПРОСТРАНСТВО, ВРЕМЯ И ФУНДАМЕНТАЛЬНЫЕ ВЗАИМОДЕЙСТВИЯ, 2020, N 1, c. 53-65

3. Фомин И. В., Червон С.В., Махарадж С.Д. Применение уравнения Шредингера в космологии со скалярным полем на основе точных решений. ПРОСТРАНСТВО, ВРЕМЯ И ФУНДАМЕНТАЛЬНЫЕ ВЗАИМОДЕЙСТВИЯ, 2020, N 2

4. Igor Fomin, and Sergey Chervon. Exact and Slow-Roll Solutions for Exponential Power-Law Inflation Connected with Modified Gravity and Observational Constraints. Univers, 2020, 2020, 6, 199; doi:10.3390/universe6110199

5. Is the Axionic Dark Matter an Equilibrium System? Alexander B. Balakin and Amir F. Shakirzyanov. Universe 2020, 6, 192; doi:10.3390/universe6110192

6. Alexander Balakin  and Gleb Kiselev. Spontaneous Color Polarization as A Modus Originis of the Dynamic Aether. Universe 2020, 6, 95; doi:10.3390/universe6070095

7. Viktor Zhuravlev and Sergey Chervon. Qualitative Analysis of the Dynamics of a
Two-Component Chiral Cosmological Model. Universe 2020, 6, 195; doi:10.3390/universe6110195
 

1. Качественный анализ динамики космологических моделей

1.1. Динамика двухкомпонентной киральной космологической модели

1.1.1. Введение

Киральные космологические модели (ККМ) представляют собой самогравитирующие нелинейные сигма модели с потенциалом взаимодействия при их рассмотрении в космологических пространствах-временах \cite{Chervon:2013gm}. Киральные космологические модели, как и мультиполевые модели со скалярными полями  \cite{Chervon:2019prd}, являются естественным обобщением полевых моделей с одним скалярным полем (обзор точных решений см., например, в работах \cite{Chervon:2017kgn},\cite{Fomin:2017xlx} и в монографии \cite{Chervon:2019sey}). Особенность ККМ заключается в том, что в них учитывается потенциальное и кинетическое взаимодействие между полями, которое, насколько нам известно, до последнего времени было восстановлено на основе анализа наблюдательных данных только в работе \cite{ChervAbb}.

1.1.2. Динамическая система 2-ККМ

Двух-компонентная ККМ с диагональной метрикой кирального пространства [17] имеет вид: $$S=\frac{1}{2\kappa}\int R\sqrt{-g}d^4x +\int\left(\frac{1}{2}h_{11}\phi_{,i}\phi^{,i}+ \frac{1}{2}h_{22}(\phi,\psi)\psi_{,i}\psi^{,i} -V(\phi,\psi)\right)\sqrt{-g}d^4x.$$ Здесь $h_{11}={\rm const}$ и $h_{22}(\phi,\psi)$ - метрические коэффициенты внутреннего пространства полей с интервалом:
$$ds^2_{in} = h_{11}(d\phi)^2+h_{22}(\phi,\psi)(d\psi)^2.$$ Основные уравнения 2-ККМ в пространственно-плоской метрике Фридмана-Робертсона-Уокера (ФРУ)
$$dS^2= dt^2 - a(t)^2\left(dx^2+dy^2+dz^2\right)$$ имеют следующий вид:
$$h_{11}\Big(\ddot{\phi}+3H\dot{\phi}\Big)-\frac{1}{2}\frac{\partial h_{22}}{\partial\phi}\dot{\psi}^2+\frac{\partial V}{\partial\phi}=0,$$ $$3Hh_{22}\dot{\psi}+\frac{\partial}{\partial t}\Big(h_{22}\dot{\psi}\Big)-\frac{1}{2}\frac{\partial h_{22}}{\partial \psi}\dot{\psi}^2+\frac{\partial V}{\partial \psi}=0,$$ $$H^2=\frac{\kappa}{3}\left(\frac{1}{2} h_{22}\dot{\psi}^2+\frac{1}{2} h_{11}\dot{\phi}^2+V\right),\tag{1.1}\label{EqNSM}$$ $$\dot{H}=-\kappa\Big(\frac{1}{2} h_{22}\dot{\psi}^2+\frac{1}{2} h_{11}\dot{\phi}^2\Big).$$ Первые два уравнения этой системы представляют собой уравнения киральных полей, а два последних являются уравнениями Эйнштейна-Фридмана.

В дальнейшем будем полагать, что данные уравнения записаны в безразмерном виде. Предполагается, что безразмерные переменные имеют такой вид: $$t=\tau/T_0, \phi=\phi_{d}/\phi_0, H = H_{d}/H_0, a = a_{d}/a_0, V=V_{d}/V_{0},~\kappa=\kappa_{d}/\kappa_{0}.$$ Здесь величины с индексом $d$ обозначают размерные величины, а с индексом $0$ - масштабные коэффициенты той же размерности. Для того, чтобы безразмерная система приобрела вид уравнений (\ref{EqNSM}) необходимо, чтобы масштабные коэффициенты были бы связаны следующими соотношениями: $$H_0T_0=1, V_0=\phi_0^2T_0^2, \kappa_p=\phi_0^2$$ Кроме этого, используя произвол  в выборе $\phi_0^2$ в дальнейшем при численном счете будем полагать: $\kappa=1$, что эквивалентно: $\phi_0^2=\kappa_d$.

Введем для удобства дальнейшего аналлиза следующие новые переменные: $\xi=h_{11}\dot{\phi}$ и $\eta=h_{22}(\phi,\psi)\dot{\psi}$. В этих новых переменных уравнения поля будут выглядеть следующим образом: $$\dot{\xi}+3H\xi+\frac{1}{2}\eta^2\frac{\partial}{\partial \phi}\frac{1}{h_{22}}+\frac{\partial V}{\partial \phi}=0,\tag{1.2}\label{Eqxi}$$ $$\dot{\eta}+3H\eta+\frac{1}{2}\eta^2\frac{\partial}{\partial \psi}\frac{1}{h_{22}}+\frac{\partial V}{\partial \psi}=0.\tag{1.3}\label{Eqeta}$$

Умножая первое уравнение на $\dot{\phi}$, а второе на $\dot{\psi}$, и складывая результаты, приходим к следующему уравнению:$$\frac{d}{dt}\left[\left(\frac{\xi^2}{h_{11}}+\frac{\eta^2}{h_{22}}\right)a^6\right]+2a^6\frac{d}{dt}{\cal V}(t)=0.\tag{1.4}\label{EqcV1}$$ Здесь ${\cal V}$ - потенциал самодействия, как функция времени: ${\cal V}(t)=V(\phi(t),\psi(t))$.

Третье уравнение системы (\ref{EqNSM}) можно в новых переменных записать следующим образом: $$H^2=\frac{\kappa}{6}\left(\frac{1}{h_{22}}\eta^2+\frac{1}{h_{11}}\xi^2+2V\right).\tag{1.5}\label{HppV}$$ Отсюда находим: $$\frac{1}{h_{22}}\eta^2+\frac{1}{h_{11}}\xi^2= \frac{6}{\kappa}H^2-2V.$$

Подставляя это соотношение в (\ref{EqcV1}), окончательной приходим к следующему соотношению: $${\cal V} = \frac{1}{3\kappa}\frac{\ddot{b}}{b},$$ где $b=a^3$.

Комбинируя третье и четвертое уравнения системы (\ref{EqNSM}), приходим к следующему уравнению: $$\dot{H}+3H^2=\kappa V(\phi,\psi).\tag{1.6}\label{EqH}$$ Это уравнение является стандартным элементом космологических моделей со скалярными полями. С учетом (\ref{EqcV1}) последнее уравнение  превращается в тождество.

Для дальнейшего анализа полезно данную модель привести к стандартному виду динамической системы. Учитывая, что одно из полевых уравнений является следствием трех остальных уравнений, мы включим в динамическую систему уравнения (\ref{Eqxi}) и (\ref{Eqeta}), уравнение (\ref{EqH}), а также третье уравнение системы (\ref{EqNSM}).

В качестве динамических переменных системы выберем следующие: $H, \xi=h_{11}\dot{\phi},\eta=h_{22}\dot{\psi},~\phi,~\psi,~ a$.

Систему уравнений можно теперь привести к следующему виду: $$\dot{H}+3H^2=\kappa V(\phi,\psi),$$ $$\dot{\xi}+3H\xi-\frac{1}{2}\frac{\eta^2}{h^2_{22}}\frac{\partial h_{22}}{\partial \phi}+\frac{\partial V}{\partial \phi}=0,\tag{1.7}\label{EqDynSys6}$$ $$\dot{\eta}+3H\eta-\frac{1}{2}\frac{\eta^2}{h^2_{22}}\frac{\partial h_{22}}{\partial \psi}+\frac{\partial V}{\partial \psi}=0,$$ $$\dot{\phi}=\xi/h_{11},~~\dot{\psi}=\eta/h_{22}(\phi,\psi),~~\dot{a}=Ha.$$ Данная система представляет собой шестимерную динамическую систему, для которой cоотношение (\ref{HppV}) представляет интеграл движения.

1.1.3. Особые точки моделей 2-ККМ

Построенная система (\ref{EqDynSys6}) позволяет провести общий анализ динамики двух-компонентных ККМ, а также качественный анализ их асимптотического поведения.

Во первых, обратим внимание на первое уравнение системы (\ref{EqDynSys6}). Такую форму данное уравнение приобрело в результате комбинации уравнений Эйнштейна-Фридмана.
Предположим, что метрические коэффициенты внутреннего пространства $h_{11}$ и $h_{22}$ являются неотрицательными функциями $\psi$ и $\phi$: $$h_{11}>0,~h_{22}\ge 0.\tag{1.8}\label{CondhP}$$ Из этого условия сразу можно сделать два важных вывода. Первый вывод состоит в том, что при таком условии для всех $t$:$$\dot{H}<0.$$

1.1.2.1 Критические точки для случая $h_{22}>0$

Рассмотрим в начале ситуацию, когда функция $h_{22}(\phi,\psi)>0$, т.е. ни где не обращается в ноль. В этом случае уравнения, соответствующие неподвижным точкам, имеют вид: $$\xi_0=0,~\eta_0=0,$$ $$3H_0^2=\kappa V(\phi_0,\psi_0),\tag{1.9}\label{EqBP}$$ $$\left.\frac{\partial V}{\partial \phi}\right|_{\phi=\phi_0,\psi=\psi_0}=0,~~\left.\frac{\partial V}{\partial \psi}\right|_{\phi=\phi_0,\psi=\psi_0}=0.$$ Отсюда находим: $$H_0=\sqrt{\frac{\kappa}{3}V(\phi_0,\psi_0)},\tag{1.10}\label{SolH0}$$ где $\phi_0,\psi_0$ - значения полей в экстремумах потенциала самодействия, которые находятся из последних двух уравнений системы (\ref{EqBP}). Эти особые точки будем называть основными.  Таким образом, для всех основных особых точек значение параметра Хаббла $H_0$ определяется значением потенциала самодействия в соответствующем экстремуме.

Примером простой модели является модель с одним минимумом потенциала: $$V(\phi,\psi)=V_0+q\phi^2+p\psi^2\tag{1.11}\label{DefV22}$$ и постоянными коэффициентами $h_{11}$ и $h_{22}$. Траектории такой системы на фазовой плоскости $\phi-\psi$ представлены на рис.1. и рс. 2. На рис. 2 более подробно показана область вблизи основной особой точки. Голубым цветом отмечены начальные точки. Траектории отмечены черными пунктирными линиями. На рис. 2-6 показаны графики зависимости от времени основных динамических переменных модели. На рис. 7 представлена зависмость от времени функции $\Delta(t)$, которая служит контролем точности вычислений. Для нагладности на рис. 8 приведены фазовые траектории системы в трехмерном пространстве $\phi-\psi-H$. Расчеты проводились с помощью программы, написанной на Maple. Для численного решения с системы уравнений модели использовалась встроенная численная схема dverk78.

Рис. 1. Фазовые траектрии системы для потенциала (\ref{DefV22}). Красной точкой отмечена особая точка динамической системы, совпадающая с минимумом потенциала самодействия

Рис. 2. Фазовые траектрии системы для потенциала (\ref{DefV22}) вблизи особой точки. Красной точкой отмечена особая точка динамической системы, совпадающая с минимумом потенциала самодействия

Рис. 3. Изменение поля $\phi$ со временем для набора фазовых траекторий рис. 1

Рис. 4. Изменение поля $\psi$ со временем для набора фазовых траекторий рис. 1

Рис. 5. Изменение параметра Хаббла $H$ со временем для набора фазовых траекторий рис. 1

Рис. 6. Изменение масштабного фактора $a$ со временем для набора фазовых траекторий рис. 1

Рис. 7. Изменение отклонения интеграла движения $\Delta$ со временем для набора фазовых траекторий рис. 1

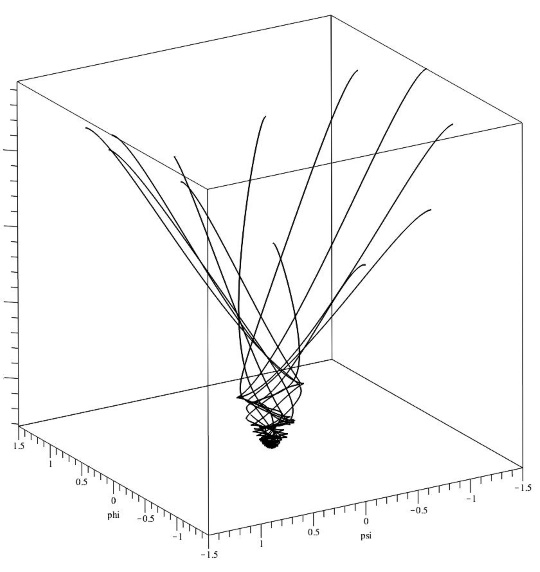
Рис. 8. Фазовые траектории системы в трехмерном пространстве $\phi-psi-H$ для набора фазовых траекторий рис. 1

1.1.2.2 Особые точки при $h_{22}\ge 0$

В случае, если в при некоторых значениях $\phi$ и $\psi$ функция $h_{22}(\phi,\psi)$ обращается в ноль, к основным особым точкам добавлются \textbf{специальные}, связанные с нулями функции $h_{22}(\phi,\psi)$. Обозначим через $\phi_s$ и $\psi_s$ значения полей, при которых:
$$h_{22}(\phi_s,\psi_s)=0.$$

Представим в окрестности точки $(\phi_s,\psi_s)$ второе и третье уравнение системы (\ref{EqDynSys6}) в таким виде: $$h^2_{22}(\dot{\xi}+3H\xi)-\frac{1}{2}\eta^2\frac{\partial h_{22}}{\partial \phi}+h^2_{22}\frac{\partial V}{\partial \phi}=0,$$ $$h^2_{22}(\dot{\eta}+3H\eta)-\frac{1}{2}\eta^2\frac{\partial h_{22}}{\partial \psi}+h^2_{22}\frac{\partial V}{\partial \psi}=0.$$ Не трудно видеть, что в этом случае в точке $(\phi_s,\psi_s)$, где $h_{22}$ обращается в ноль, последние уравнения приобретают такой вид: $$\eta^2\frac{\partial h_{22}}{\partial \phi}=0,~~\eta^2\frac{\partial h_{22}}{\partial \psi}=0.$$ Эти уравнения уже не содержат производных потенциала и автоматически обращаются в ноль при условии $\eta=0$, что является следствием других уравнений системы. Таким образом, новая особая точка не будет совпадать в общем случае ни с одной основной особой точкой, которые связаны по определенияю с минимумами потенциала самодействия. Для этих особых точек уравнения их определяющие выглядят так:
$$\xi_s=0,~\eta_s=0,$$ $$3H_s^2=kV(\phi_s,\psi_s),\tag{1.12}\label{EqSP}$$ $$h_{22}(\phi_s,\psi_s)=0.$$ В этом случае предельное значение $H_s$ определяется значением потенциала не в  экстремуме потенциала, а в специальной особой точке.

Специальные особые точки могут  составлять в пространстве функций непрерывные кривые. Многообразие возможных систуаций при этом требует отдельного анализа, который выходит за рамки данной статьи. Однако рассмотрим здесь одну простую ситуацию, которая, тем не менее, может играть важную роль в космологической динамике. Для этого рассмотрим вариант выбора $h_{22}$ следующего вида: $$h_{22}=f(\phi).\tag{1.13}\label{Defh22phi}$$ Будем предполагать, что имеется значение поля $\phi=\phi_s$, при котором: $f(\phi_s)=0$. Тогда в окрестности $\phi=\phi_s$ в пространстве полей второе и третье уравнение системы (\ref{EqDynSys6}) примут такой вид: $$f(\phi)(\dot{\xi}+3H\xi)-\frac{1}{2}\eta^2f'(\phi)+h^2_{22}\frac{\partial V}{\partial \phi}=0,$$ $$\dot{\eta}+3H\eta+\frac{\partial V}{\partial\psi}=0.$$ Последнее уравнение этой системы не содержит множителя $f(\phi)$, обращающегося в ноль в точке $\phi=\phi_s$. Следовательно, уравнения для специальной особой точки будут следующими: $$\xi_s=0,~\eta_s=0,$$ $$3H_s^2=kV(\phi_s,\psi_s),\tag{1.14}\label{EqSPphi}$$ $$f(\phi_s)=0,~~\left.\frac{\partial V}{\partial\psi}\right|_{\phi=\phi_s,\psi=\psi_s}=0.$$

1.1.3 Асимптотический анализ модели

Наличие двух типов особых точек модели основных и специальных приводит к более сложному анализу динамики в их окрестности с помощью теории возмушщения первого порядка.
В данном разделе на основе теории возмущений проводится полная классификация основных особых точек киральных моделей. Теория возмущений вблизи специальных особых точек оказывается гораздо более многообразной, чем основных, что требует отдельной работы. Поэтому в данном разделе теория возмущений применяется лишь для одного типа специальных точек, связанных с точечными нулями метрических коэффициентов кирального пространства.

1.1.3.1 Основные особые точки

Вычисляем уравнения для возмущений в первом порядке. Полагаем: $$\xi=\xi_0+v=v,~~\eta=\eta_0+w,~~\phi=\phi_0+\Phi,~~\psi=\psi_0+\Psi,~~H=H_0+\chi.$$ Здесь предполагается $|v|<<1,|w|<<1,|\Phi|<<1,|\Psi|<<1,|\chi|<<1$. Подставляя эти соотношения в исходную систему и отбрасывая слагаемые второго порядка малости, находим: $$\dot{\Phi}=v,~~~\dot{\Psi}=w,~~~\dot{\chi}=-6H_0\chi,$$ $$\dot{v}=-3H_0v - U\Phi -V\Psi,\tag{1.15}\label{EqPrtBase}$$ $$\dot{w}=-3H_0w - V\Phi -W\Psi .$$ Здесь: $$U=\left.\frac{\partial^2 V}{\partial\phi^2}\right|_{\phi_0,\psi_0},~~V=\left.\frac{\partial^2 V}{\partial \phi\partial\psi}\right|_{\phi_0,\psi_0},~~W=\left.\frac{\partial^2 V}{\partial\psi^2}\right|_{\phi_0,\psi_0}.$$ Как видно из этих соотношений, в первом порядке теории возмущений при отсутствии особенностей $h_{22}(\phi,\psi)$ параметры асимптотики полей не зависят от выбора $h_{22}(\phi,\psi)$ и $h_{11}$ .

Уравнение для $\chi$ интегриуется независимо от остальных уравнений, что дает: $$\chi=\chi_0e^{-6H_0t}.\tag{1.16}\label{Solxi}$$

Уравнения для двух переменных $\Phi$ и $\Psi$ принимают такой вид: $$\frac{d^2\Phi}{dt^2}+3H_0\frac{d\Phi}{dt}+U\Phi+V\Psi=0,$$ $$\frac{d^2\Psi}{dt^2}+3H_0\frac{d\Psi}{dt}+V\Phi+W\Psi=0.$$ Заметим, что данная система в некотром смысле является аналогом механической системы движения шарика в потенциальном поле сил. Отличием ее от такой системы является наличие специфической силы сопротивления, пропорциональной скорости шарика с декрементом затухания $3H_0$.

Отыскивая частные решения этой системы в следующем виде: $$\Phi=Ae^{\lambda t},~~\Psi=Be^{\lambda t},$$ приходим к следующей алгебраической системе уравнений: $$\lambda^2A+3H_0A\lambda+UA+VB=0,~~~\lambda^2B+3H_0B\lambda+VA+WB=0.$$ В результате характеристическое уравнение для $\zeta=(\lambda+3H_0/2)^2$ можно записать в следующем виде:$$ (\zeta+U_1)(\zeta+W_1)-V^2=0,$$ где введены обозначения: $$U_1=U-\frac{9}{4}H_0^2,~~W_1=W-\frac{9}{4}H_0^2.$$ Отсюда находим: $$\zeta_{1,2}=\Big(\lambda+3H_0/2\Big)^2=-\frac{1}{2}(U_1+W_1)\pm\sqrt{(U_1-W_1)^2+4V^2}.$$ Окончательно, характеристические числа имеют вида: $$\lambda_{1,2} = -\frac{3}{2}H_0\pm \frac{1}{\sqrt{2}}\sqrt{-(U_1+W_1)+D_0} = -\frac{3}{2}H_0\pm \frac{1}{\sqrt{2}}\sqrt{D_0-S_0},$$ $$\lambda_{3,4} = -\frac{3}{2}H_0\pm\frac{1}{\sqrt{2}}\sqrt{-(U_1+W_1)-D_0}=
    -\frac{3}{2}H_0\pm\frac{1}{\sqrt{2}}\sqrt{-D_0-S_0}.$$ Здесь $D_0=\sqrt{(U_1-W_1)^2+4V^2}=\sqrt{(U-W)^2+4V^2}\ge 0$ и $S_0=U_1+W_1=U+W-\frac{9}{2}H_0^2$.
Отсюда следует, что в зависимости от вида квадратичной формы потенциала самодействия вблизи экстремумов имеются несколько различных типов поведения решений. Эти варианты определяются значениями собственных чисел. Значения же собственных чисел определяются соотношениями между $D_0$ и величиной $S_0$.

Все возможные ситуации распадаются два общих класса. Первый класс, обозначим через $A$. В него будем включать все варианты особых точек, значение потенциала самодействия в которых отлично от нуля и положительно: $V(\phi_0,\psi_0)>0$. В этом случае асимптотическое значение $H_0$ отлично от нуля, что означает, что Вселенная выходит асимптотически на стадию экспоненциального расширения.

Второй класс, обозначаемый далее через $B$, соответствует нулевому значению потенциала самодействия в особой точке и нулевому асимптотическому значению параметра Хаббла: $H_0=0$. Этот вариант означает $\dot{a}=0$, т.е. асимптотически масштабный фактор $a$ выходит на некоторое постоянное значение $a_0$.

1.1.3.2 Класс $A$ основных особых точек

Рассмотрим класс $A$ особых точек. Тогда существуют следующие варианты основных особых точек в этом классе.

$\underline{I.  S_0>D_0>0}$
 Это условие означает: $$U+W > D_0+\frac{9}{2}H_0^2.$$ В этом случае: $$\lambda_{1,2} = -\frac{3}{2}H_0\pm i\frac{1}{\sqrt{2}}\sqrt{S_0-D_0},~~\lambda_{3,4} = -\frac{3}{2}H_0\pm i\frac{1}{\sqrt{2}}\sqrt{S_0+D_0}. $$  Все собственные числа имеют отрицательную вещественную часть. Это означает, что на фазовой плоскости данные неподвижные точки являются устойчивыми фокусами. Поскольку одновременно мнимая часть собственных чисел не обращается в ноль, эти точки не могут быть узлами.

$\underline{II. D_0>S_0>0}$
    В этом случае имеем: $$D_0+\frac{9}{2}H_0^2 > U+W >0.$$
    Собственные числа уравнения для возмущений будут такими: $$\lambda_{1,2} = -\frac{3}{2}H_0\pm \frac{1}{\sqrt{2}}\sqrt{D_0-S_0},~~\lambda_{3,4} = -\frac{3}{2}H_0\pm i\frac{1}{\sqrt{2}}\sqrt{D_0+S_0}.$$  Первые два корня вещественные, но среди них могут быть как отрицательные, так и положительные, что означает в общем случае неустойчивость данных точек. Для того, чтобы все же данные точки были устойчивыми, достаточно, чтобы выполнялось дополнительное условие: $$\frac{1}{\sqrt{2}}\sqrt{D_0-S_0} < \frac{3}{2}H_0.$$ В последнем случае точки будут фокусами. При этом особая точка может совпадать с седловой точкой потенциала. Последнее отличает данную динамическую систему от механической модели скатывания шарика в минимум потенциальной ямы.

$\underline{III. ~~S_0<0}$
    При выполнении такого условия: $$U+W <\frac{9}{2}H_0^2.$$ В этом случае: $$ \lambda_{1,2} = -\frac{3}{2}H_0\pm \frac{1}{\sqrt{2}}\sqrt{|S_0|+D_0},~~\lambda_{3,4} = -\frac{3}{2}H_0\pm \frac{1}{\sqrt{2}}\sqrt{D_0-|S_0|}$$  Этот вариант распадается на два дополнительных варианта.

 $\underline{III a. ~~S_0<0, D_0>|S_0|}$
     Собственные числа  в этом варианте таковы: $$\lambda_{1,2} = -\frac{3}{2}H_0\pm \frac{1}{\sqrt{2}}\sqrt{|S_0|+D_0},~~\lambda_{3,4} = -\frac{3}{2}H_0\pm \frac{1}{\sqrt{2}}\sqrt{D_0-|S_0|}$$ Все собственные числа - вещественные. Для устойчивости необходимо, чтобы все четыре числа были отрицательными. Однако это не возможно в силу того, что $|S_0|>0$. Это означает, что все такие точки не устойчивы.

     $\underline{III. b ~~S_0<0, D_0\le|S_0|}$

     Собственные числа в этом варианте таковы: $$\lambda_{1,2} = -\frac{3}{2}H_0\pm \frac{1}{\sqrt{2}}\sqrt{|S_0|+D_0},~~\lambda_{3,4} = -\frac{3}{2}H_0\pm i\frac{1}{\sqrt{2}}\sqrt{|S_0|-D_0}$$ В этом случае условие устойчивости сводится к одному дополнительному условию:$$    \sqrt{|S_0|+D_0} < \frac{3 \sqrt{2}}{2}H_0.$$  Точка будет фокусом.

Общий вывод состоит в том, что в классе $A$ при всех вариантах не вырожденной квадратичной формы потенциала вблизи особой точки в случае ее устойчивости она будет фокусом. Исключением является случай $S_0=D_0=0$. В этом случае особая точка будет узлом, а не фокусом. Для этого требуется, чтобы: $$U=W, ~~ U=\frac{3}{4}k V(\phi_0,\psi_0)>0.$$  Последнее означает, что точка является минимумом потенциала, сам потенциал вблизи особой точки имеет симметричную квадратичную форму ($U=W$), а его значение определяется второй производной $U$ в этой точке.

1.1.3.3 Класс $B$ основных особых точек

    В классе $B$ особых точек собственные числа вычисляются следующим образом: $$\lambda_{1,2} = \pm \frac{1}{\sqrt{2}}\sqrt{-(U+W)+D_0} =\pm \frac{1}{\sqrt{2}}\sqrt{D_0-S_0},$$ $$\lambda_{3,4} = \pm\frac{1}{\sqrt{2}}\sqrt{-(U+W)-D_0}=\pm\frac{1}{\sqrt{2}}\sqrt{-D_0-S_0}.$$  Здесь $D_0=\sqrt{(U_1-W_1)^2+4V^2}=\sqrt{(U-W)^2+4V^2}\ge 0$ и $S_0=U+W$.

В этом классе почти полностью воспроизводятся варианты класса $A$. Отличием является вариант $I$.

$\underline{I. S_0>D_0>0}$

    В этом случае: $$\lambda_{1,2} = \pm i\frac{1}{\sqrt{2}}\sqrt{S_0-D_0},~~\lambda_{3,4} = \pm i\frac{1}{\sqrt{2}}\sqrt{S_0+D_0}. $$ Это означает, что все собственные числа чисто мнимые,  особая точка совпадает с минимумом потенциала и является центром. В классе $A$ этот вариант соответствует фокусу.

$\underline{II. D_0>S_0>0}$

    В этом случае особая точка совпадает с седловой точкой потенциала и при всех других условиях является не устойчивой. В классе $A$ седловая потенциала точка может оказаться фокусом.

$\underline{III. ~~S_0<0}$

     Поскольку в этом случае $$U+W <0,$$ особая точка совпадает либо с седловой точкой, либо с максимумом потенциала.  Собственные числа при этом будут такими: $$\lambda_{1,2} = \pm \frac{1}{\sqrt{2}}\sqrt{|S_0|+D_0},~~\lambda_{3,4} = \pm \frac{1}{\sqrt{2}}\sqrt{D_0-|S_0|}$$   Хотя бы одно из этих чисел оказывается вещественным с положительной вещественной частью. Это означает, что такие особые точки - неустойчивые.

Рассмотренные варианты асимптотического поведения системы описывают лишь основные возможности. Существует несколько особых вариантов поведения системы в некоторых особых ситуациях. Первой такой ситуацией является случай, когда потенциал самодействия всюду равен нулю $V=0$. В этом ситуации имеем:  $$D_0=\sqrt{(U_1-W_1)^2}=|U_1-W_1|=|U-W|.$$ Кроме этого, в пределе $t\to\infty$ параметр Хаббла стремится к нулю, что приводит к степенной инфляции или фридмановскому режиму расширения, что требует отдельного анализа.

    Еще одной важной особенностью данной системы является возможность возникновения особых точек, связанных с такими значениями полей, при которых метрический коэффициент $h_{22}(\phi,\psi)$  обращается в ноль. Анализ поведения системы вблизи этой точки оказывается сложным. Однако далее будет показано, что в такой точке может возникать дополнительная притягивающая точка на фазовой плоскости.

1.1.4. Специальные особые точки

    Анализ поведения исследуемой системы вблизи специальных особых точек даже в первом порядке теории возмущений представляет собой сложную задачу анализа уравнений в порядках теории возмущений больше первого. Поэтому в данной работе мы не будем рассматривать все возможные варианты специальных особых точек. Вместо этого мы проанализируем лишь один важный вариант выбора функции $h_{22}$ в виде (\ref{Defh22phi}). Более того в данной работе мы ограничимся выбором: $$h_{22}=\phi^2,$$ что соответствует плоскому внутреннему киральному пространству, в котором поле $\phi$ играет роль радиальной координаты, а $\psi$ - угловой для полярной системы координат.

    Квадрат элемент длины в этом пространстве будет иметь стандартный вид: $$ d\sigma^2=d\phi^2+\phi^2d\psi^2.$$  При этом мы будем предполагать, что минимум потенциала смещен от точки $\phi=0,~\psi=0$. В противном случае анализ задачи также усложняется и не будет демонстрировать то особое поведение системы в рассматриваемой ситуации, которое мы хотим проиллюстрировать далее численным счетом.

 Поскольку $h_{22}$ зависит только от $\phi$, то система уравнений для возмущений примет такой вид: $$\dot{\Phi}=v,~~~\dot{\Psi}=w,~~~\dot{\chi}=-6H_s\chi,$$ $$K_1w^2=-U_s(K_1\Phi+K_2\Psi)^2,\tag{1.17}\label{EqPrtPec}$$ $$\dot{w}=-3H_0w - V_s\Phi -W_s\Psi .$$ Здесь введены обозначения: $$U_s=\left.\frac{\partial V}{\partial \phi}\right|_{\phi_s,\psi_s},~~V_s=\left.\frac{\partial^2 V}{\partial \phi\partial\psi}\right|_{\phi_s,\psi_s},~~W_s=\left.\frac{\partial^2 V}{\partial \psi^2}\right|_{\phi_s,\psi_s},$$ $$K_1=\left.\frac{\partial h_{22}}{\partial \phi}\right|_{\phi_s,\psi_s},~~K_2=\left.\frac{\partial h_{22}}{\partial \psi}\right|_{\phi_s,\psi_s}.$$   Все производные вычисляются в специальной особой точке с координатами $\phi_s,\psi_s$, в которой выполняются уравнения (\ref{EqSPphi}). В рассматриваемом случае $\phi_s=0$, а $\psi_s$ определяется из условия: $$\left.\frac{\partial V}{\partial \psi}\right|_{\phi=\phi_s,\psi=\psi_s}=0. $$  В четвертом уравнении системы (\ref{EqPrtPec}) оставлены слагаемые наибольшего второго порядка. Слагаемых первого порядка это уравнение не содержит.

В случае выбора $f(\phi)=\phi^2$ имеем: $\phi_s=0$. В этой точке: $$K_1=\left.\frac{\partial h_{22}}{\partial \phi}\right|_{\phi_s,\psi_s}=2\phi_s=0,~~K_2=\left.\frac{\partial h_{22}}{\partial \psi}\right|_{\phi_s,\psi_s}=0.$$ Поэтому четвертое уравнение системы (\ref{EqPrtPec}) обращается тождественно в ноль. Следовательно, необходимо рассматривать это уравнение в третьем порядке. В третьем порядке это уравнение сводится к условию: $$\Phi\Psi^2=0.$$ Не тривиальным является только одно решение: $\Phi=0$. В этом случае вблизи специальной особой точки примет относительно возмущений первого порядка поля $\psi$ такой вид: $$\dot{\Psi}=w,~~~\dot{\chi}=-6H_s\chi,\tag{1.18}\label{EqPrtPec1}$$ $$\ddot{\Psi}=-3H_0\dot{\Psi} - W_s\Psi .$$ Следовательно, при приближении к специальной особой точке осциллировать будет только поле $\psi$.

1.1.4 Модель с массивными полями

    Рассмотрим в качестве первой нелинейной сигма-модели модель с потенциалом, соответствующим стандартной массивной теории. Именно, рассмотрим потенциал следующего вида: $$V(\phi,\psi)=V_0+\mu^2_{1}(\phi-P)^2+\mu^2_{2}(\psi-Q)^2.$$  Здесь $P$ и $Q$ - вещественные числа определяющие положение минимума потенциала на плоскости $(\phi,\psi)$. Число $V_0>0$ - определяет значение потенциала в минимуме, а параметры $\mu_1$ и $\mu_2$ характеризуют значения массы квантов скалярных полей.

1.1.4.1 Модель с $h_{22}>0$

    Параметры метрики кирального пространства выберем в следующем виде: $h_{11}=1$, $h_{22}=\exp(q\psi)$. Без труда находим, что данная модель имеет единcтвенную неподвижную точку $\phi_0=P,~~\psi_0=Q$, которая является устойчивым фокусом. Согласно ранее проведенному анализу функция $h_{22}=\exp(q\psi)$ ни где не обращается в ноль (возможно только на бесконечности), поэтому специальных особых точек в данном варианте модели не существует.

    Пример поведения такой модели представлен на рис.  . Модель соответствует выбору потенциала: $$V(\phi,\psi)=1.0+4\phi^2+8\psi^2,~~P=Q=0,\tag{1.19}\label{DefV00}$$ и метрического коэффициента $h_{22}=e^{-\psi}$.

На рисунках (\ref{Pic0V})-(\ref{Pic0H}) представлены графики поведения параметров модели вблизи особой точки для значений параметров $V_0=0.25,~m_1^2=4,~~m_2^2=8,~~q=-0.5$.

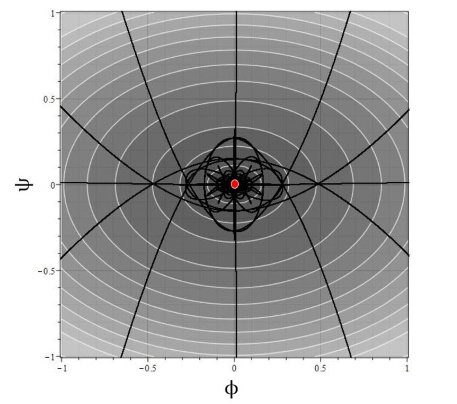
    Изолинии потенциала самодействия на плоскости $(\phi,\psi)$ представлены на рис. 9a,b. Для сравнения на рис. (9a) приведен фазовый портрет системы для случая $h_{22}=1$ (эквивалентно рис. 1), а на рис. (9b) фазовый портрет с тем же потенциалом, но с $h_{22}=e^{-\psi}$.

Рис. 9. Фазовый портрет динамической системы для модели с потенциалом (\ref{DefV00}): a) для случая $h_{22}=1$, b) для случая $h_{22}=e^{-\psi}$ .

Зависимость параметров моделей от времени и соответствующий фазовый портрет приведены на рис. (\ref{PicPPt}).

a

b

Рис. 10. Зависимость поля $\phi$ от $t$ для модели с потенциалом (\ref{DefV00}): a - модель с $h_{22}=1$, b - $h_{22}=e^{-\psi}$.

a

b

Рис. 11. Зависимость  поля $\psi$ от $t$ для модели с потенциалом (\ref{DefV00}): a - модель с $h_{22}=1$, b - $h_{22}=e^{-\psi}$.

a

b

Рис. 12. Зависимость  параметра Хаббла $H$ от $t$ для модели с потенциалом (\ref{DefV00}): a - модель с $h_{22}=1$, b - $h_{22}=e^{-\psi}$.

1.1.4.2 Модель с $h_{22}=(\phi-0.5)^2$

    В качестве первого примера модели, в которой кроме основной точки есть и одна специальная, рассмотрим модель с потенциалом (\ref{DefV00}): $$V(\phi,\psi)=1.0+4\phi^2+8\psi^2,\tag{1.20}\label{DefV12}$$  но со смещенным минимумом в точку $P=0,~Q=0$. При этом функциональный вид метрического коэффициента $h_{22}$ выберем в следующем виде: $$h_{22}(\phi,\psi)=\phi^2.\tag{1.21}\label{Defh22phi2}$$  В этом случае специальная особая точка появляется в точке с координатами $\phi_s=1,~\psi_s=0$.
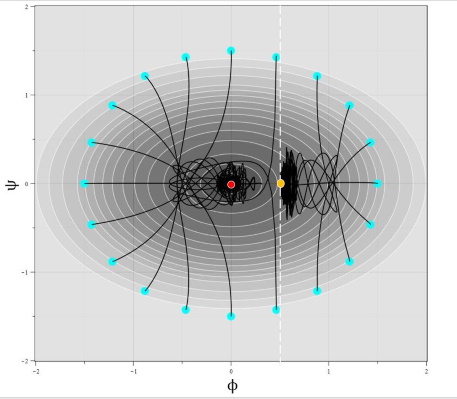
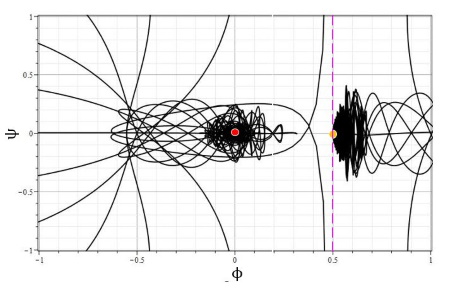
     Поведение параметров модели для разлиных начальных условий представлено на рис. 13-14.

a

b
 

Рис. 13. Фазовый портрет системы для модели с $h_{22}=(\phi-0.5)^2$: a) - вместе с изолиниями потенциала, b - область вблизи особых точек. Красным указана основная особая точка, а желтым - специальная. Вертикальная пунктирная линия - прямая $\phi=0.5$ на плоскости $\phi-\psi$

a

b

c

d

Рис. 14. Зависмость от времени поля $\phi$ (a), поля $\psi$ (b), параметра Хаббла $H$ (c) и интеграла движения $\Delta$ (d) для модели с с $h_{22}=(\phi-0.5)^2$.

Не трудно видеть, что фазовые кривые на плоскости $(\phi,\psi)$ в зависимости от положения начальной точки стремятся при $t\to\infty$ к обоим особым точкам. Если в начальной точке $\phi_0>0.5$, фазовые траектории сходятся к специальной особой точке, а в случае $\phi<0.5$ - к  основной. Специфичность специальной особой точки состоит  в том, что ее тип не возможно охарактеризовать с помощью стандартных определений: узел, центр, фокус, седло. Как было показано, при приближении к рассматриваемой специальной особой точке осциллирует в первом порядке только одно поле, что отличает ситуацию и от притягивающего узла и от притягивающего фокуса. Более того, притягивающей эта точка является только в полуплоскости $\phi>0.5$, а в полуплоскости $\phi<0.5,$ эта точка выглядит как седло. Поэтому эту точку  трудно охарактеризовать даже терминами ``полуфокус'', ``полуцентр'' или ``полуседло''.  Для такого поведения модели на плоскости $(\phi,\psi)$ можно предложить простую механическую аналогию, которая упоминалась при анализе основных особых точек. Наблюдаемая динамика аналогична скатыванию шарика в яму под действием силы тяготения при наличии сил трения. В случае отсутствия нулей у функции $h_{22}(\phi,\psi)$ при конечных значениях $\phi$ и $\psi$ скатывание при всех начальных положениях шарика ведет к основному минимуму. Наличие же нулей у функции $h_{22}(\phi,\psi)$ аналогично появлению непреодолимых барьеров для движения шарика. В результате по аналогии с шариком поля "скатываются" к условному минимуму потенциальной энергии, находящемся на барьере, который на рис. 13 изображен вертикальной пунктирной линией. Эта аналогия иллюстрирует стремление всех траекторий в модели с $h_{22}=(\phi-0.5)^2$ при $\phi_0>0.5$ к условному минимуму потенциала в точке $\phi_0=0.5,~\psi_0=0$. Это поведение, по всей видимости, воспроизводится и при более сложных структурах нулей функции $h_{22}(\phi,\psi)$. Однако это требует отдельного анализа, выходящего за рамки данной статьи.

    Заметим также, что анализ фазовых кривых на плоскости $\phi-\psi$ (см. рис. 13) , а также изменений полей со временем на рис. 14 (a,b) демонстрирует осцилляции поля $\psi$ вблизи специальной особой точки при почти полном отсутствии осцилляций поля $\phi$, что полностью согласуется с формулой (\ref{EqPrtPec1}), полученной ранее для специальной особой точки рассматриваемого здесь типа.

Как демонстрируют графики зависимости $H=H(t)$ и $H=H(\phi,\psi)$ асимптотическое поведение параметра Хаббла существенным образом зависит от особой точки, к которой движется система в зависимости от начальных условий. Графики, приведенные на рис. 14c, показывают, что вычисленные заранее асимптотические значения параметра Хаббла полностью  совпадают с их численным значением. График на рис. 14c показывает, что построенные решения найдены с высокой точностью поскольку расчеты проводились с помощью процедуры dverk78 математического пакета Maple, использующей метод Рунге-Кутта 7-8 порядков.

Рассмотрим второй пример, показывающий аналогичное поведение модели, но с более сложным потенциалом следующего вида: $$V(\phi,\psi)=150-4(\phi-1)^2-8(\psi-2)^2+\phi^4+\psi^4.\tag{1.21} \label{DefVphi4}$$   Этот потенциал имеет один минимум в точке $\phi_0=-1.769292354, ~~\psi_0=2.649435914$. Как и в предыдущем случае $h_{22}=\phi^2$. Соответствующие графики изменения параметров модели со временем представлены на рис.
 
    Как и на рис. \ref{Pic1V}  на рис.  \ref{Pic2V} вертикальной пунктирной линией изображен ``барьер'', на котором лежит специальная особая точка. В соответствие с уравнениями системы \rf{EqPrtPec1} вблизи специальной особой точки осциллирует только поле $\psi$. Это хорошо видно из графиков на рис. \rf{Pic2PPt}, которые иллюстрируют эволюцию полей вблизи специальной особой точки. На графиках \rf{Pic2V} осцилляции поля $\psi$ малы и поэтому мало заметны.  На рис. (\ref{Pic2H}) приведены графики зависимости параметра Хаббла от времени и значений интеграла движения. Расчеты для модели c потенциалом (\ref{DefVphi4}) проводились с помощью процедуры ck45 математического пакета Maple, использующего метод Рунге-Кутта 4-5 порядков (использование процедуры dverk78 приводит для данной модели к более раннему обрыву вычислений вблизи особых точек).

1.2. Динамика космологической модели в обобщенной тензорно-скалярной теории гравитации с потенциалом Хиггса