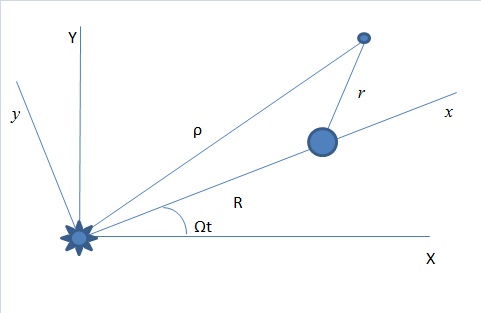
 Рис.1
Рис.1
Наступило суперлуние! А когда следующее? Над теорией движения Луны трудились настоящие титаны механики. В итоге мы имеем машинные теории. Потому, что уравнения движения Луны, выведенные титанами не интегрируются.
Луна в сущности является маятником с подвижной точкой подвеса. В нулевом, так сказать, приближении уравнения движения Луны можно получить, решив ограниченную задачу трех тел. Луна в этой задаче не имеет массы, а Земля движется строго по окружности. Интересен сам по себе вопрос, как влияет движение точки подвеса (т.е. Земли) на орбитальные характеристики Луны. Какой была бы орбита Луны, если бы Земля покоилась?
Запишем основной закон динамики для нашей системы в подвижных осях координат (Рис.1)
Уравнения движения выглядят так:
.jpg) (1)
(1)
Астрономические константы мы можем взять здесь:http://www.sai.msu.ru/neb/rw/cm_const.htm
Уравнения движения, аналогичные (1) можно увидеть в [1]
Зависимость расстояния Земля-Луна от времени, рассчитанная по ф-лам (1) приведена на Рис. 2. Луна стартует с высоты 350 000 км от поверхности Земли с почти круговой скоростью.
.jpg)
Рис. 2.
Это знакомая специалистам по Луне картина "дыхания" апогей-перигей.
Итак, если бы Земля покоилась, Луна могла бы двигаться по почти круговой орбите с апогеем 350 000 км (начальная скорость 97% от круговой). Годовое движение Земли поднимает орбиту Луны аж до 380 000 км. Такова мощь сил инерции. Гироскопические силы сдвигают перигей и апогей в пространстве, заставляя орбиту Луны прецессировать.
Другими словами, чтобы Луна двигалась так, как она движется сейчас, нужно было припарковать ее к Земле по ходу движения с внешней стороны орбиты Земли на расстоянии 350 000 км тормознув до 97% круговой геоцентрической скорости. Отклонение в доли процентов по высоте и скорости катастрофически меняют картину движения.
Гармонический анализ функции r(t) показывает наличие трех частот: аномалистической частоты, эвекционной частоты и их суммы.
Чтобы получить зависимость r(t) непосредственно, запишем уравнения Лагранжа для обобщенных координат r и "тета" (угол между вектором r и осью X). Уравнения движения имеют следующий вид:
.jpg) (2)
(2)
Вопрос об их интегрируемости остается пока открытым. Возможно, математики найдут способ выразить три частоты r(t) через астрономические константы.
Источники информации
[1]Аналитическая динамика. Парс Л.А., Главная редакция физико-математической литературы изд-ва «Наука», 1971 г., 636 стр.

- Ingus's блог
- Войдите на сайт для отправки комментариев
- 8397 просмотров


