
This research has made use of NASA's Astrophysics Data System
Луна в своем движении вокруг Солнца совершает довольно сложные маневры, пересекая орбиту Земли. Можно подумать, что ее траектория напоминает синусоиду, наложенную на эллипс. Но тогда местами кривизна траектории становится положительной, т.е. выпуклой в сторону Солнца, что существенно нарушает баланс сил инерции и гравитации.
Решение этого непростого вопроса я нашел в статье столетней давности
Title: The Moon's Orbit Around the Sun
Authors: Turner, A. B.
Journal: Journal of the Royal Astronomical Society of Canada, Vol. 6, p.117
Bibliographic Code: 1912JRASC...6..117T
http://adsabs.harvard.edu/full/1912JRASC...6..117T
Позволю себе процитировать ее целиком
Перевод таков:
Мы привыкли думать о Луне как принадлежащей исключительно Земле и описывающей за год волнистый путь по отношению к орбите Земли. Очевидно, такая орбита Луны будет вогнутой в сторону солнца с 1-ой четверти до полной луной в 3-ей четверти и выпуклой с 3-го четверти через новолуние до первой четверти, а в некоторых старых книгах по астрономии, это было неправильно представлены таким образом. (Рис. 1).

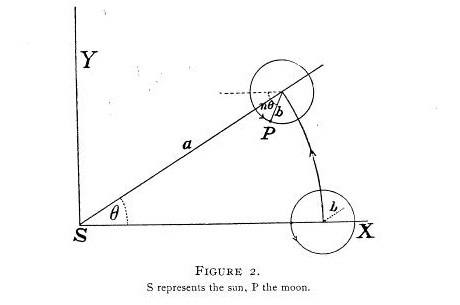
Благодаря, однако, тому факту, что расстояние Луны от Земли очень мало по сравнению с расстоянием Земли от Солнца (около 1/400), а также тому, что она делает около 13 оборотов вокруг Земли в год, то лучше рассмотреть путь Луны, как тело описывающее орбиту вокруг Солнца, которая постоянно слегка возмущена притяжением Земли. Такой путь всегда будет вогнутым к солнцу, но близок к орбите Земли, пересекая ее два раза в месяц. Приближенное математическое решение задачи получено в предположении, что Земля движется по окружности, а орбита Луны представляет собой круг в той же плоскости. Возьмем Солнце в начале координат, пусть а радиус орбиты первого, с периодом Т. и b радиус орбиты спутника, с периодом Т / n, движущегося в той же плоскости. Начальные координаты спутника возьмем в фазе «новой» Луны, дальнейшее движение будет таким:
Рис 2.
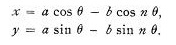
Теперь радиус кривизны определяется по формуле
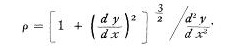
Дифференцируя и подставляя мы находим, что для любой точки Р пути спутника
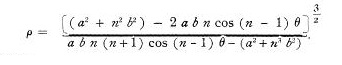
Когда …
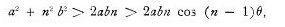
числитель всегда вещественный и положительный, а знак р зависит от знака знаменателя.
Три случая будут рассмотрены...
На этом я остановлюсь.
Я проверил правильность выкладок. Они верны. Но расчет по ним сделан автором не совсем точно.
Расчет в среде MathCad дает следующие результаты:
Орбита Луны практически не отличима от овала, кривизна которого не меняет знак, а вогнутость всегда обращена к Солнцу.
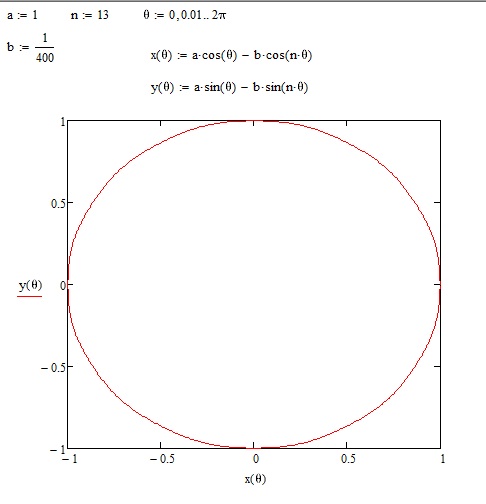
Это подтверждает и расчет по приведенной формуле для радиуса кривизны:
Итак, в новолуние радиус кривизны гелиоцентрической орбиты Луны составляет 1,621 а.е., а в полнолуние 0,749 а.е. (здесь Тёрнер ошибся). Теперь, если мы посчитаем баланс сил инерции, гравитации Земли и гравитации Солнца, то окажется, что несмотря на двойной перевес солнечной гравитации к земной, дисбаланс с силами инерции составит порядка 5% от от гравитации к Земле. При этом дисбаланс носит сжимающий характер, т.е. в полнолуние и новолуние он прижимает лунную гелиоцентрическую орбиту к земной.
- Ingus's блог
- Войдите на сайт для отправки комментариев
- 37044 просмотра


.JPG)
.JPG)


Удивительное дело!
Луна не уходит к Солнцу, летает вокруг Земли - а ей упорно приписывают траекторию околосолнечную. Почему в таком случае спутникам Марса не приписывают подобные траектории. или Юпитерианским?
Есть система Земля-Луна, и она входит в систему Солнечную, как и все остальные планеты. И пора уж это понять и принять.
Другое дело. что Луна идет вокруг Земли несколько необычно, захватывая две разрешенные орбиты - да. Напоминая траекторию кометы. Но связано это скорее всего с тем, что ее диаметр больше, чем ширина максимальной разрешенной орбиты - 400000х0,005 = 2000км.
Ох, друзья, простите! Оказывается, я невнимательна - и к другим планетам и их спутникам применяют эту теорию. Слушайте, да вы эзотерики еще те!
Как может планета, у которой притяжение ниже, чем Солнечное, что-то удерживать около себя? Если Солнце тянет к себе Луну вдвое сильнее, чем Земля - то луна давно уже должна была у бежать от нас.
Уважаемый Иван Евгеньевич!
Я решил применить данную модель к расчету скорости спутника Юпитера ИО.
Параметры взял следующие:
$a=778548900000$
$b=421700000$
$n=2448,98$
$\omega = \frac{2\pi}{4332.59*86400}$
Диапазон гелиоцентрической скорости спутника у меня получается 4.26648 - 30.4022 км/с.
для $t=0:864*T_Io:864000$, где $T_Io=1,7691$ - период спутника в земных солнечных сутках.
Что скажете?
Десятичную точку переставил. Повнимательней надо бы
Благодарю. А у меня не получается исправлять, когда уже есть ответ на запись. Вы наверное модератор?
У вас должна быть кнопка "Изменить". Она располагается ниже окна с редактируемым текстом. Можно сказать, что я модератор.
Так я же и говорю: пока комментарий свежий, кнопка изменить есть, но как только на него кто-то ответил, она пропадает, остается только "ответить" и "цитировать". Кстати, цитирование тут работает не очень уверенно, иногда совсем не работает...
Попрошу администратора проверить Ваши замечания по работе сайта. Спасибо!
На сайте такое количество комментариев к одной статье превышает запрограммированные ранее возможности комментирования.
Уважаемые Ingus и Stupa ! Мы поддерживаем Ваш взаимный интерес и предлагаем перенести дальнейшие обсуждения в комментарии к другим статьям Ingus-а. Это не должно нарушить логику Вашего обсуждения, особенно если сообщить, что переходите на другую ветку. Многие с интересом наблюдают ход Ваших мыслей.
P.S. Ваша переписка лишний раз доказывает, что любой увлеченный труд находит единомышленников. Этот сайт дал возможность проявить себя многим талантливым авторам и идеям.
Похоже, но размерность скорости надо исправить с км/c на м/с. Орбитальная скорость Ио 17.33 км/c, а Юпитера - 13.07 км/c. Складываем и вычистаем, получаем Ваш результат.
Средняя скорость Юпитера 13.07 км/с. Так что похоже на правду.
Сделал рассчет для Титана:
Параметры взял следующие:
$a=1433449369500$
$b=1221870000$
$n=674,77$
$\omega = \frac{2\pi}{10759,22*86400}$
Диапазон гелиоцентрической скорости спутника у меня получается 4,17 - 15,26 км/с.
А подобная амплитуда вас не смущает? Что такое "орбиатльная скорость Ио = 17,334 км/с"? Тут ведь вероятно имеется в виду иовицентрическая скорость, или она таки гелиоцентрическая? Почему в википедии она указана как постоянная? Ведь даже относительно Юпитера она очевидно должна быть переменной. И как она может быть столь существенно быстрее орбитальной скорости самого Юпитера? Например, для Луны в википедии указана средняя скорость 1,023км/с.
Я посчитал для Каллисто, там диапазон получается тоже немаленький 4,865-21,265 км/с. Можно как-то оценить влияние подобных перепадов скорости на тело спутника? Особенно с учетом того, что происходят они в течение нескольких земных дней, т.е. за весьма короткий промежуток времени.
Не может ли быть ошибки в построении нашей рабочей "эмпирической" модели?
Эксцентриситет орбиты Ио 0,0041. О чем это говорит? Его планетоцентрическая скорость практически постоянна.
Вас удивляет, что планетоцентрическая скорость спутника выше гелиоцентрической самой планеты? Что ей мешает быть выше? Какой закон? Представьте себе гонки по кругу на авианосце. Что мешает машине выжать на спидометре большую цифру, чем у авианосца?))
Что такое перепад скорости? Ускорение. Как ускорение влияет на тело, находящееся в невесомости? Мы снова приходим к модели приливных явлений. Нужно рассматривать Ио как твердое тело под действием двух притягивающих центров. Как там его растягивает и сжимает, вопрос непростой.
На счет невесомости на орбите Юпитера трудно сказать. Есть вероятность, что там не полная невесомость, особенно с учётом такой скорости. Судя по всему влияние Юпитера на таком незначительном расстоянии велико весьма. Можно ли сказать, что Юпитер мечтает стать коричневым карликом?
Давайте попробуем вернуться к задаче с ускорениями, а то мы как-то её забросили. Хотя бы на примере Луны. Вообще же орбита Юпитера очень интересна. Еще более - орбита Урана.
А на эту тему нет никаких уже сделанных изысканий? Кстати, Чеботарев мне очень понравился. Читаю с удовольствием.
Уважаемый Иван Евгеньевич!
Сердечно поздравляю Вас с Новым годом и Рождеством Христовым и желаю Вам новых научных открытий и откровений. Я убеждён, что "гранит" науки таит в себе еще немало "золота" и Вам вполне под силу будет его оттуда извлечь.
Благодарю Вас за уделенное мне внимание и надеюсь, что наша корреспонденция будет и Вам хоть чем-то полезна.
Тимофей (aka Stupa)
Благодарю Тимофей Александрович! С Новым годом и Рождеством Христовым и Вас поздравляю. Всегда приятно с Вами пообщаться.
По моменту импульса.
$\overline L=m \overline \rho \times \overline v$
Как перемножить векторы я, пожалуй, разберусь. Но чему они равны?
И. Правильно ли я понимаю, что мы тут ищем момент импульса Луны в гелиоцентрической системе отсчета?
Вот в википедии читаем:
"На орбите момент импульса распределяется между моментами импульса собственного вращения планеты и её орбитального движения:
$L_{total} = L_{spin} + L_{orbit}$"
В таком случае для Луны необходимо добавить еще один момент:
$L_{total} = L_{spin} + L_{orbit} + L_{dev}$
где $L_{dev}$ - момент импульса Луны в ее движении относительно орбиты Земли, в том смысле, что она не просто движется по орбите (солнечной), которая по сути совпадает с орбитой Земли, но также с известной периодичностью отклоняется от этой орбиты.
Давайте Луну считать точкой. Работаем в гелиоцентрической системе.
Т.е. Вы предлагаете принебречь массой Луны и ее собственным осевым вращением? Взять только расстояние до Солнца и (переменную) орбитальную скорость и расмотреть их векторное произведение? Орбиту Луны Вы тоже предлагаете "спрямить" до Земной?
Правильно я понимаю, что
$\overline \rho (x,y)$, где
Правильно.
Или все-таки:
$\overline \rho (x,y)$, где
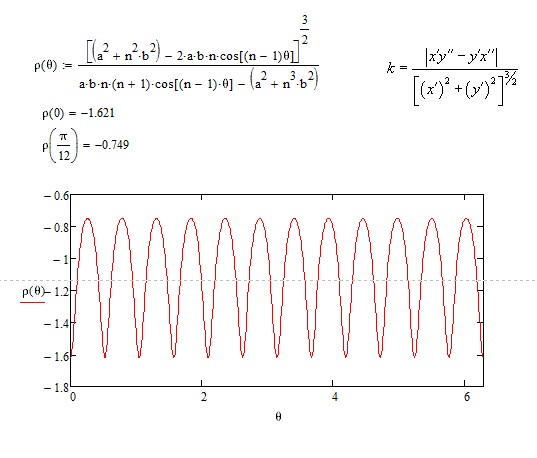
$x = acos(\omega t)-bcos(n\omega t)$
$y = asin(\omega t)-bsin(n\omega t)$
$\overline v (\dot x, \dot y)$, где
А произведение в итоге должно получиться:
$L = m [\overline p,\overline v] = m \left | \left | x\dot y \right |-\left | \dot x y \right |\right |$
так?
Осталось перемножить все синусы-косинусы и вывести формулу. Вдруг момент не будет зависеть от времени?
Да. Так лучше. Я проглядел Вашу ошибку в предыдущем посте)
У меня получается:
$L = m( a^{2}\omega+b^{2}n\omega-(1+n)(ab\omega cos(\omega t + n\omega t)))$
У меня немного иначе... Проверьте еще раз..
$L = m (a^{2}\omega+b^{2}n\omega-(1+n)ab\omega cos(\omega t - n\omega t))$
ДА, конечно, на бумажке так и написано, переписал с ошибкой.
Итак, момент импульса гелиоцентрической луны зависит от времени, т.е. не постоянный.
А что если теперь учесть вращение Луны вокруг своей оси? Не поможет оно скомпенсировать переменность? Впрочем, вряд ли, оно ведь постоянное... А вот движение относительно орбиты Земли, вверх-вниз относительно плоскости эклиптики?
Какое движение вверх-вниз? У нас же плоская постановка задачи.
Кстати. Мы допустили, что центр Земли движется по окружности... А ведь он тоже "вихляется"...
Иван Евгеньевич! Мне кажется, я понял, куда девается импульс. Я размышляю так:
Итак Луна движется относительно Земли не равномерно, "внутри" земной орбиты медленнее, а снаружи "быстрее". При этом она продолжает оставаться повернутой к Земле одной и той же стороной. Это значит, что на внутренней стороне орбиты Земли она должна вращаться медленнее, а на внешней - быстрее. Соответственно, если мы добавим к орбитальному импульсу осевой, он должен первый уравновесить. Как Вы считаете?
"Вихляние" Земли, я думаю, на импульс Луны оказывает мало влияния. Но с учетом вышесказанного, надо допустить, что угловая скорость Земли тоже неравномерна, хотя этого "практически" незаметно.
Момент импульса никуда не "девается". Он сохраняется. В среднем. Константа плюс гармоника.
Мы рассчитали момент импульса Луны, через координаты и скорость Луны. Однако при расчете координат Луны мы полагали, что Земля движется по окружности. Но это не так. Размах "вихляний" около 9000 км, если не ошибаюсь. Мы не должны рассуждать. Мы должны считать, а потом рассуждать. Нужно сравнить момент импульса собственного вращения Луны с ее орбитальным моментом. Также нужно оценить клад "вихляния" Земли в расчет орбитального момента Луны.
9000 км - это слишком мало. Для 940 млн км земной орбиты, даже для 400 тыс км расстояния до Луны, 9000 - это ничто. Вклад этих вихляний в момент импульса Луны, полагаю, слишком мал, хотя, разумеется, должен быть. Согласен, однако, что надо учесть все факторы и все посчитать.
А вы не согласны, что осевое вращение Луны может быть неравномерным?
Я могу составить свое мнение о равномерности вращения Луны только после того, как составлю дифур ее движения как твердого тела в гравитационном поле двух центров притяжения... Я этого еще не делал. Можно конечно рассмотреть один притягивающий центр... Землю... или Солнце. К чему она тянется сильнее:)? Но скорее всего надо рассматривать оба центра.
Да, это интересная задача. Ведь это поможет понять, почему Луна движется подобным образом? Почему притормаживает и ускоряется?
По поводу ускорения.
Мы взяли вторые производные:
$\ddot x = bn^{2}\omega ^{2}cos(n\omega t)-a\omega ^{2}cos(\omega t)$
так, что
$\overline \rho=(x,y)$
$\overline a_{m-s}=(\frac{G M_s}{(x^2+y^2)^{3/2}} x, \frac{G M_s}{(x^2+y^2)^{3/2} }y)$
$\overline r=(x_1,y_1)$
$\overline a_{m-e}=(\frac{G M_e}{(x_1^2+y_1^2)^{3/2}} x_1, \frac{G M_e}{(x_1^2+y_1^2)^{3/2} }y_1)$, где
$x_1=x-a \cos\theta$
$y_1=y-a \sin\theta$
Как все это увязать?
Я никак не могу понять, каким образом в векторной форме определить точки квадратур и сизигий, если у нас там не фигурирует $n$.
Вы уж простите слабость моей физ-мат подготовки, я вообще больше гуманитарий, а образование у меня экономическое, но мне хочется разобраться и я стараюсь как могу. В целом мне понятен ход мысли и направление поиска, но в практических аспектах навыка не хватает.
Напрасно Вы пасуете. Вы можете стать специалистом по системам ДУ) И я могу Вам в этом помочь.
Хм. Заманчивое предложение. Готов попробовать. Я просто не знаю, с чего начать и с какой стороный подойти.
Для начала, нам нужна задача, интересная Вам, которая подразумевает составление дифференциальных уравнений. В моем случае это был сферический маятник, потом задача двух тел, потом задача трех тел, потом движение твердого тела в гравитационном поле...
Что придумать, чтобы потребовалось заняться дифурами, мне пока даже в голову не приходит. Я подумаю. Что если, например, попытаться ввести в наши "эмпирические" формулы еще и третью координату, относительно оси z, т. е. плоскости эклиптики? Еще интересно рассмотреть подобным же образом движение спутников Урана с учетом наклона его оси. Там ведь спутники движутся в плоскости практически перпендикулярной плоскости орбиты. Соответственно, там и исходные "эмпирические" формулы должны быть несколько иными? Вообще, интересно разобраться со спутниками всех газовых гигантов, с их резонансами...
Меня, признаться, больше занимает другая задача. Вот существует 5 систем небесных координат, из них первые четыре - геоцентрические, а пятная - галактическая. Почему не существует гелиоцентрической системы координат???
Я так до конца и не понимаю, что делать с ускорениями. Подставлять в формулы реальные значения масс и углов? В какой форме мы должны получить ответ - как отношение двух целых чисел?
Если спутник планеты движется перпендикулярно плоскости орбиты планеты, работает эффект Лидова-Козаи. Математика у него сложная, но я предлагаю ее упростить... Было бы интерсно.
Гелиоцентрические координаты существуют!:)
Ускорения мы пока оставим. Давайте закончим с векторным произведением и моментом импульса Луны.
Вы шутите: по ссылке эклиптические координаты, они геоцентрические, как бы их ни называли. Как я уже писал, под гелиоцентрическими я предлагаю понимать координаты, в которых базовой плоскостью является плоскость солнечного экватора. Мне кажется, мы увидим интересную картину, если кеплеровы элементы орбит планет и их спутников для всей СС приведем к такому общему знаменателю, как плоскость солнечного экватора.
Уран из всех планет СС, конечно, очень интересен своей нетрадиционной ориентацией, и сутники его тоже, соответственно. Жаль в стеллариуме нельзя посмотреть на планетарную систему "со стороны", так, чтобы выбрать точку наблюдения за пределами планеты на определенном от нее расстоянии и понаблюдать за взаимным перемещением небесных тел и их траекториями.
По моменту импульса прошу уточнить выше.
Это я просмотрел. На рисунке-то - обычная эклиптическая. Конечно, если центром считать центр Солнца, система должна быть гелиоцентрической. Тогда поясните (из википедии):
7,155° (отн. солнечного экватора)[4], 1,57869° (отн. инвариантной плоскости)[4]
348,73936°[2]
В какой это системе?
Вообще, меня как раз интересовал этот вопрос: как ДВУ Земли может отличаться от 0, если система отсчета эклиптическая?
Хотя, поразмыслив, скажу вот что: базовой плоскостью выбрана плоскость эклиптики, значит обе они геоцентрические. Для гелиоцентрической системы координат, как я у же говорил, базовой плоскостью должна быть плоскость солнечного экватора. Эклиптика должна иметь к этой плоскости указанное выше наклонение.
Центраьной точкой считается Солнце. И при этом система геоцентрическая? Класс. Куда смотрят модераторы Википедии?))
Может нам обратиться к Дубошину? Он покруче Википедии будет...
Представьте себе, что вы прибыли в систему Арктура. Вы видите 12 планетарных орбит. И хотите сориентироваться в них. Предлагаемая вами эклиптическая система координат вам поможет? Где на Арктуре вы возьмете плоскость эклиптики? Или вы хотите за таковую принять орбиту третьей от звезды планеты? Зачем?
Я не предлагаю никаких систем. Я работаю в той, что мне удобна и все!
Ну и в случае с Арктуром, какую систему координат Вы бы выбрали как наиболее удобную?
А какую задачу надо решить у Арктура?
PS
Пора переходить в ЖЖ.
У Арктура нужно составить карту арктурианской СС, определеить параметры орбит планет.
Дело в том, что основаня проблема с гелиоцентрической системой, о которой я говорю, это собственно определение солнечного экватора. Эту плоскость мы можем определить только условно, со значительной погрешностью. Поэтому и придумали инвариантную плоскость; но и ее тоже не так-то просто установить. Поэтому, конечно, эклиптика нам ближе и понятнее, и пока мы "не собираемся" на другие планеты, нам ее вполне достаточно. Вот и получается, что от геоцентрики мы не можем уйти никуда, мы привязаны к Земле намертво, и телом, и сознанием.
ПС Давно уже жду Вас в ЖЖ. Вы зайдите хотя б.
ППС Так что с моментом импульса, верно посчитал?
Просто там речь идет о том, что плоскость плоскость эклиптики проходит через две точки - центр Земли и центр Солнца. Это очевидно. В любой сферической системе координат обязательно должна быть базовая плоскость. Эклиптика - это плоскость орбиты Земли, так? Раз за базовую плоскость приняли ее, значит, и система геоцентрическая. Иными словами, вместо плоскости солнечного экватора, которая, разумеется, проходит и через центр Солнца но не совпадает с эклиптикой, приняли за базовую - эклиптику.
Вы ответьте, пожалуста, мне на вопрос, как в эклиптической системе ДВУ Земли может быть отлична от 0?
Помните, я задавал вопрос по поводу орбиты Марса? Это все из той же оперы. У нас все орбиты приведены к эклиптике. Понятно, что находясь на Земле, нам так удобнее. Но с точки зрения СС это некорректно: тут все расчеты должны быть привязаны к Солнцу.
Если можно обратиться к кому-то, кто покруче википедии, я только за!
Тимофей Александрович, посмотрите Вот эту книгу, может найдете там полезное?
http://eqworld.ipmnet.ru/ru/library/mechanics/celestial.htm
Чеботарев Г.А. Аналитические и численные методы небесной механики. М.-Л.: Наука, 1965 (djvu)
Тимофей Александрович, посмотрите Вот эту книгу, может найдете там полезное?
http://eqworld.ipmnet.ru/ru/library/mechanics/celestial.htm
Чеботарев Г.А. Аналитические и численные методы небесной механики. М.-Л.: Наука, 1965 (djvu)
Отвечаю. Долгота восходящего узла орбиты Земли посчитана по небесному экватору. Кстати, как должна изменяться долгота восходящего узла орбиты Земли из-за прецесии?
Википедия: "Долгота́ восходя́щего узла́ — один из основных элементов орбиты, используемый для математического описания ориентации плоскости орбиты относительно базовой плоскости. Определяет угол в базовой плоскости, образуемый между базовым направлением на нулевую точку и направлением на точку восходящего узла орбиты, в которой орбита пересекает базовую плоскость в направлении с юга на север. Для определения восходящего и нисходящего узла выбирают некоторую (так называемую базовую) плоскость, содержащую притягивающий центр. В качестве базовой обычно используют плоскость эклиптики (движение планет, комет, астероидоввокруг Солнца), плоскость экватора планеты (движение спутников вокруг планеты) и т. д. Нулевая точка — Первая точка Овна (точка весеннего равноденствия). Угол измеряется от направления на нулевую точку против часовой стрелки."
Базовая плоскость - это плоскость эклиптики. Она же - плоскость орбиты. Какой же может быть угол между базовой плоскостью и плоскостью орбиты? А если ДВУ считается в экваториальной системе координат, почему она называется долгота а не прямое восхождение?
На Ваш вопрос: я думаю, что ДВУ должна также прецессировать вместе с осью.
Я имел ввиду увеличивается или уменьшается?
Поскольку ТВР смещается вдоль эклиптики в направлении орбитального движения Земли, а ДВУ измеряется от ТВР в ту же сторону, соответственно она должна уменьшаться.
Хорошо бы увидеть это на картинке.. Слова дают плохую картинку.
Согласен. Но когда я смотрю на вот эту картинку: Кеплеровы_элементы_орбиты, я не понимаю, как это изобразить, ибо тут показаны две плоскости, которые в случае Земли должны совпадать.
Вас не затруднит разобраться, как они вычисляют долготу восходящего узла Земли? http://articles.adsabs.harvard.edu/cgi-bin/nph-iarticle_query?db_key=AST&bibcode=1994A%26A...282..663S&letter=.&classic=YES&defaultprint=YES&whole_paper=YES&page=663&epage=663&send=Send+PDF&filetype=.pdf
Вычисляют через прецессию и наклонение на J2000, если я правильно понимаю.
Но меня интересует не то, как "они" вычисляют, а как "они" определяют. Я вполне доверяю справочникам относительно точных значений элементов орбит, вопрос у меня в другом. Мне кажется, Вы либо не не понимаете, либо не хотите понять, что я имею в виду.
Недопонимание присутствует. Так как они определяют? Есть это в статье? Я не читал просто.
Берут текущий наклон оси (obliquity) $\epsilon_0$ и прецессию $P_1$ за 1000 лет, и фиксируют эпоху J2000.
Для вычисления вековых смещений (secular variations) вводят две переменных $sin \pi sin \Pi$ и $sin \pi cos \Pi$, где $\pi$ - наклонение эклиптики, а $\Pi$ - ДВУ.
Из этих данных вычисляют среднюю эклиптику на дату относительно фиксированной эклиптики J2000.
Далее считают производные относительно масс планет и относительно констант $\epsilon_0$ и $P_1$ и вычисляют погрешности.
Как-то так.
Выходит ДВУ определяют по отношению к эклиптике эпохи J2000?
Или Вы хотите сказать, что есть две эклиптики - на эпоху J2000, и текущая, и их пересечением определяется линия узлов Земли?
Насколько я понимаю, ДВУ Земли служит отправной точкой для вычисления прецессии. Как и наклонение. ТВР постоянно смещается из-за прецессии, чтобы знать долготу ТВР нужна какая-то точка отсчета, за таковую и принимают ДВУ. Я только не понимаю физический смысл ДВУ Земли, ведь тут плоскость орбиты и плоскость эклиптики совпадают. Откуда же берется у орбиты Земли линия узлов?
С цитатами я тоже не силен тут. Вы не путайте нашу модель с реальным положением дел! n мы выбрали произвольно... примерно так сказать.
Ускорение через координаты это суть сумма ускорений Земли к Солнцу и Луны к Земле. Направлено оно ни к Солнцу, ни к Земле.
Поэтому, чтобы найти ускорение к Солнцу, пишем через силы. Силы-то точно уж направлены, одна к Солнцу, одна к Земле.
ДУ решать не будем. Будем считать, что за нас их решили и нашли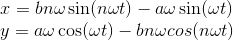
Моя "ошибка" идёт отсюда. Видимо, Вы имели в виду, что координаты, которые "нашли за нас" такие:
$x = acos(\omega t)-bcos(n\omega t)$
$y = asin(\omega t)-bsin(n\omega t)$
Ведь то, что Вы указываете, это уже первая производная.
Точно. Проклятая копипаста!) Вот что отличает настоящих ученых от нас с Вами. Вот такие косяки)
В смысле, настоящие ученые своих косяков не видят? Или наоборот, у них без косяков - как без пряников?
ПС. Мне кажется, или на самом деле не все мои сообщения Вы успеваете прочесть? Я оставляю сразу по нескольку комментов и они раскиданы по странице: форум тут не очень юзер-френдли.
Да.. Похоже я их не все нахожу.
Выше см. результат по моменту импульса.
Ниже см. соображения по поводу СТО.
По поводу ереси не очень понимаю, что из приведенных выше цитат "оскорбляет" Ваши "чувства верующего". Разве не очевидно, что существует жесткая иерархия: галактика (центр галактики) - звездная система (звезда) - элемент звездной системы (планеты, спутники и т.п.). Разве есть соменения в том, что без Солнца не было бы и всей СС? Разве Луна в первую очередь не элемент СС, а после уж - спутник Земли? Очевидно ведь, что основным (если не сказать единтсвенным) источником энергии для планет (и их спутников) является звезда.
Вообще любопытно, что в данном контексте вы прибегаете к религиозной терминологии. Действительно, в последние годы наука приобретает множество сходных черт с религией: все больше положений науки приходится принимать на веру. Теория БВ, например.
Вот! Это предельно важно, ИМХО.
Общаясь с учеными из самых различных сфер, я пришел к выводу, что в основе современной науки отсутствует целостная философская система. А без нее наука как без рук. Философия позитивизма себя исчерпала и скомрометировала еще в прошлом, если не сказать в позапрошлом веке. Коммунизм дал нам диамат. Но и тот не выдержал пробы временем. Сегодня же, по меткому выражению одного знакомого ученого, единственная философия науки это "tenure track", проще говоря, бабло.
А проблема тут вот в чем. Например, определие ЖИЗНИ как таковой, через "метаболизм" и т.п. слишком узко. Для материальных форм, возможно, это до некоторой степени приемлемо, да и то с оговорками. Но есть же еще и мета-физика. Не знаю, будете ли вы настаивать, что сознание - это функция материи, или все-таки согласитесь, что сознание - надматериально? А ведь это базовые вещи. Если относительно этого у нас нет ясной картины, то все остальные определения, которые мы выводим из этих первичных категорий, теряют смысл.
В контексте планеты - нам важно определить, является ли планета живым организмом, или это всего лишь сгусток абстрактной материи, хаотическим образом самоорганизовавшийся из некоей протоматерии, которая досталась нам в наследство от БВ. Такой подход оставляет слишком много открытых вопросов, которые мы старательно пытаемся изолировать и не замечать. Например, а что же было за момент до БВ? ГДЕ происходит БВ? Почему он происходит? И т.д. Как насчет множественности БВ? Откуда у нас может быть уверенность, что тот БВ в поле которого живем мы, единственный во вселенной?
Современные ученые, судя даже по фильмам с того же Discovery channel, всё-таки готовы признать, что Земля - это живой организм. Не такой, как, скажем, человеческое тело, по форме и в деталях, но живой в том же смысле - обладающий собственным индивидуальным бытием. Всем очевидно, что человек создан из элементов Земли, но если Земля - это неживая материя, то как она может быть источником жизни? И если так, то значит источник жизни находится за пределами Земли? Где? Говорят, что "жизнь" на планету занесли "метеоры". Хорошо, но откуда? И там-то она откуда взялась?
Для меня, например, очевидно, что именно Солнце "родило" планеты. И их спутники. Как - это уже другой вопрос. Вы же не станете спорить, что, как я уже говорил, именно Солнце является источником энергии (читай, жизни) нашей планеты и, в частности, всего, что находится на ее поверхности. Если Солнце "выключить" - планеты не будет. Ни Земли, ни Юпитера, ни Плутона, ни Луны, ни даже Цереры. Вся энергия, которой мы располагаем, приходит к нам от Солнца. Из нее сотканы все наши атомы, нейтроны, протоны, электроны и прочие "бозоны". Ну, может быть, что-то "долетает" и от других звезд, и даже из Центра галактики, но в основном, Солнце - это наше все. Солнце - это наша вода, это микроэлементы, это электромагнитное поле и т.д. Солнце - это основа жизни, даже если под "жизнью" Вы готовы признать исключительно материальные компоненты.
Тот факт, что СС организована определенным образом, а именно: эллипсы орбит, орбитальные скорости, наклоны осей вращения и самое осевое вращение планет - все это говорит о том, что в основе этого всего лежит некий стройный закон. Исходя из понимания именно этого факта, мы верим, что все звездные системы устроены одинаково, хотя мы никогда там не были и даже в "трубу" этого не видели. Этот закон нам не понятен до конца, но он точно есть, и все наши "научные гипотезы" - это попытки осмыслить этот закон, который существует до и помимо нашего понимания, независимо от него. Как планета существует до нашего рождения и, судя по всему, останется на орбите после нашей сметри (если мы своими руками не взорвем ее, конечно).
Солнечная система - это именно организм: устроенный определенным образом, имеющий стройный вид. И планеты в нем играют роль "органов". То, что нам не понятна роль планет в жизни СС, говорит только об узости нашего кругозора и о нашем нежелании/неспособности признавать очевидные вещи.
Обсуждать современных ученых стоит, если Вы сами являетесь ученым. Иначе, это подобно тому, как сидя на диване обыватель кричит в экран: - Ну куда ты бьешь! Ну как ты бегаешь, колченогий ты футболист!
А ты выйди и забей)
Есть масса недоучившихся людей, опровергунов, альтов, которые прочитав учебник по физике за шестой класс, уверенно критикуют СТО. Уверен, что Вы не такой. Но здесь тонкая грань, за которую можно неосторожно ступить.
Солнечная система самоорганизовалась благодаря закону всемирного тяготения. Второй закон Ньютона позволяет рассчитывать все движения планет, включая прецессию и нутацию осей вращения. Приливные явления объясняются градиентом гравитационного поля. Единство и борьба противоположностей: инерции и гравитации.
Я не обсуждаю современных ученых. Предметом моего исследования являются факты окружающей действительности, которые я пытаюсь переосмыслить в философском ключе с позиции здравого смысла.
По поводу СТО у меня есть свои соображения, я готов поделиться, если вам интересно. Но они также скорее философские, нежели научные. Я - не ученый, вы же видите. И, знаете, со стороны иногда видны вещи, которые не видно изнутри. Так, вот мы смотрим на Фумальгаут и видим там аккреционный диск. А вокруг Солнца мы его не видим, только предполагаем наличие некоего подобия такого диска, который называем поясом Койпера. Но мы ничего не можем об этом поясе сказать уверенно, ни его состав, ни протяженность нам не видны. Будь мы на Фумальгауте, рассматривая Солнце, мы скорее разглядели бы это пояс более детально, нежели нам видится отсюда, изнутри. Собственно, мы предполагаем наличие у Солнца такого диска, потому что прежде мы у других звезд его разглядели. Иначе нам скорее всего и в голову бы не пришло даже предполагать его наличие.
Так и с наукой. Ученые - это своего рода каста посвященных, чтобы войти в нее, необходимо "присягнуть" на верность науке, признать опрелделенные постулаты, согласиться с некоторыми гипотезами. Причем все это приходится принимать на веру, потому что никаких доказательств добыть невозможно; как недавно сказал по телевизору Ковальчук по поводу БВ - "Его ведь никто не видел"... Это просто гипотеза, она удобна, потому что предлагает модель, которая может объяснить некоторые вещи, только и всего. Но эта гипотеза объясняя одно, заходит в тупик относительно другого, и все это знают. Мне, как неспециалисту, который на верность науке не присягал, никто не мешает относиться к ней критически и сомневаться в ее соответствии реальности. Впрочем, и Вам никто не мешает сомневаться, только я еще могу позволить себе высказываться на этот счет, а Вы вынуждены стоять на страже, иначе вас товарищи по "профсоюзу" не поймут.
В самоорганизацию СС я не верю. Законы Ньютона - это модель, которая требует определенных допущений. На заданном масштабе - в рамках СС - она дает уверенные результаты, но она же и ограничивает нашу возможность видеть более общие законы, частным случаем которых является сама. Это как если бы мы научились ремонтировать кран в ванной, заменять у него прокладки, даже за неимением заводских прокладок вырезать самостоятельно из куска резины свои. И в своей ванной мы становимся хозяевами и властителями, потому что одни и те же действия дают гарантированный результат. При этом нас не особо беспокоет, откуда в кране берется вода. И тем более нас не волнует, откуда вода берется в принципе, изначально.
Честно говоря, мне не удобно высказывать подобные соображения в этом форуме, Вашим коллегам, да и Вам все это может показаться не слишком тактичным, и вы будете правы. Тут я лезу в чужой монастырь со своей критикой. А вот в ЖЖ вы больше не заходите?
Альты - это вроде кшатриев? Похоже мы с вами из одной касты, рыбак рыбака найдет даже на безрыбье... По поводу уровня моей философии - очень здравый вопрос. Могу выслать вам пару моих статей. Вот недавно вышла книга Ю.В.Мамлеева "Россия Вечаня" с моим предисловием. Думаю, все эти вещи всё же удобнее через ЖЖ. Давайте на этом форме придержимся формата.
"Бог создал мир из ничего" и модель БВ бесконечно далеки друг от друга. Скажем так, БВ - это попытка атеистов вывести бытие из ничего без участия Бога. Кстати, Бог создал мир вовсе не из ничего. Вы читали А.Ф.Лосева "Диалектика мифа"? Исключительно рекомендую.
Про СТО книг я не читал. Посоветуете? Но я скажу Вам, что меня в ней смущает. Прежде всего - абсолютизация пространства-времени Минковского. Я считаю, что эта модель не выдерживает вообще никакой критики. В природе НЕТ никаких осей координат. Кроме того, вообще не понятно, что тут подразумевается под временем. На сегодняшний день нет вообще ни одного внятного объяснения, что такое есть время. Попытка впихнуть его в пространство при помощи еще одной мнимой оси не выдерживает критики. Далее, однородность вакуума. Крайне спорная гипотеза. Однородного вакуума не существует, во всяком случае его никто никогда нигде не фиксировал. Наконец, скорость света. Попробуем допустить, что скорость света - величина переменная, и вся ТО разваливатся. Как вам понравится такой каламбур:
$c=\sqrt{\frac{E}{m}}$
По поводу воды на Марсе: откуда у вас уверенность, что там её нет? Вы её там искали? Лично у меня нет сомнений, что она там есть. Ее просто нет на поверхности. А на поверхности ее нет потому, что марсова луна уничтожена как целостное космическое тело. Некому "выманивать" воду на поверхность. Вы как египтолог, должны понимать, что Луна и вода имеют родственную связь.
Бальмонт чудесен.
Физика пространства-времени, Тейлор Э.Ф., Уилер Д.А., 1971.
Без прочтения хотя бы одного первоисточника нет смысла обсуждать СТО. СТО это модель. Просто модель. И критику она выдержала. Это не значит, что мир именно такой. Скорость света не постоянна, как и скорость звука. Но ни одно возмущение, ни одна волна не может распространяться с бесконечной скоростью. Скорости есть предел. Можно думать, что мир это бесконечное трехмерное пространство сквозь которое течет однородное по всему пространству и равномерное время. Однако есть и другое мнение. В каждой точке пространства течет свой поток времени. Пространство с временем сплавлено в Простремя, метрика которого неевклидова (минус перед четвертой координатой). Эксперименты с быстролетящими частицами подтверждают релятивистсикие эффекты. Это все, что нужно знать. Ну и дефект массы при ядерных реакциях подтверждает закон превращения массы в энергию))
Возможно вода на Марсе есть. Мне нравится Ваша идея про марсову луну. Давайте подгоним Марсу его Луну. Заскучал Бог Войны. Она разогреет его как следует) Его железное сердце разгорится и расплавится, появится магнитное поле, кора треснет и на поверхность выйдет вода. Наклон оси у Марса примерно такой же как у Земли, поэтому климатический градиент будет умеренным. Вот только как быть с атмосферой? Гравитация слаба, чтоб удержать хороший слой... Хотя.. может растворить кислород в чем-то более тяжелом, чем азот? Или и так сойдет, просто толщина воздушного слоя будет поменьше...
Все, что Вы говрите по поводу по поводу СТО, верно только в рамках определённых допущений. При этом, как я уже говорил, нет ясности определений: что такое время, что такое пространство, что такое свет. Когда Вы говорите "течет поток времени", что конкретно Вы имеете в виду? Дело в том, что как раз эти вопросы и являются предметами моего исследования, я пишу книгу про... время. И я Вам скажу со своей колокольни: никакого потока времени не существует. Что такое поток? - это некоторая совокупность некоторых частиц, их направленное движение. Попробуйте определить частицы, которые составляют поток времени, что конкретно течет в этом вашем потоке времени? Вы знакомы с работами Козырева по поводу субстанциальности времени? Вы с ним согласны? Лично я - нет. То же самое и по пространству. Нет никакого "общего" пространства. Мы с вами живем в пространстве планеты. Это поверхность геоида. Именно поэтому оно замкнуто и ограничено. В нашем пространстве нет ни одной параллельной линии, две любых вертикали всегда пересекаются в центре Земли, трехмерная система координат к нему в принципе неприменима. Когда начинается эта чехарда с переходом от одной ИСО к другой, все это происходит в пространстве воображения, в реальности ничего подобного нет. В реальности происходит нечто иное.
Далее свет. Что такое свет? Насколько я знаю, проблема дуализма свет так и не разрешена. Т.е. у нас фактически нет ясного понимания, что конкретно мы называем светом. Поток фотонов? Возможно, у фотонов (которых, кстати, тоже никто никогда не видел), и имеется некоторая предельная скорость. Но достаточно ли этих данных, чтобы говорить о скорости света? Фактически, "скорость света" была измерена только на Земле, в условиях земной атмосферы. Её значение для "вакуума" выведено посредством математического моделирования. В реальном вакууме реальную скорость света никто не измерял. Но более того. Здесь, на Земле, весь свет, с которым мы имеет дело - это свет Солнца. Стало быть в лучшем случае мы можем говорить о скорости солнечного света. Мы ничего не знаем о скорости света Сириуса, например, или Альдебарана. Или всё-таки свет - это волна. Тогда вопрос о скорости света переходит в вопрос о распространении волн, и тут снова критический вопрос - это среда, где эти волны распространяются. В нашем случае мы снова возвращаемся к солнечной системе, и даже не к абстрактному "межзвездному пространству", а к вполне определенному месту СС, где характеристики солнечного излучения имеют вполне определенные параметры...
И это только общие соображения. Для науки это все бред, потому что наука оперирует аксиомами, которые сама себе назначила. Я вот сейчас читаю очень любопытный труд Бурбаки "Очерки по истории математики". Он там поднимает те же вопросы: до определенного момента никто даже не пытался дать определение операции сложения или умножения. Считалось, что достаточно математичесой интуиции, чтобы решить этот вопрос. Однако оказалось, что без строго определения дальнейшие действия оказываются невозможными... Так вот в отличие от математики, в которой к концу 19 века все-таки нашли необходимым полностью отказаться от "математической интуиции" и повысить уровень требований к определениям - что в итоге вывело их на более абстрактный, интегральный уровень теории множеств - история про БВ выглядит крайне неубедительно. Потому что она базируется на понятиях, которые вообще никак не определены. Что такое ИСО? Откуда они берутся? Что является источником инерции? Когда в СТО идет речь о двух разных ИСО, что конкретно имеется в виду? Земля и Юпитер? Кстати, как быть с силой Кориолиса? В ИСО ее нет и быть не может, а по факту - есть. Значит, Земля не может в полной мере считаться ИСО? Или опять мы станем пренебрегать некоторыми "незначительными" параметрами в угоду стройности наших собственных теорий и гипотез?
Вот Вы рассуждаете о Марсе с позиции массы планеты. А что, если все-таки не в массе дело? В вашем ЖЖ вы же утверждаете, что связь между массой и гравитацией еще нельзя считать доказанной. Что такое вообще масса? Это условное понятие. Это даже не вес. Что такое один килограм вещества? Это абстракция. Как в детской загадке - что тяжелее, кг железа или кг ваты. Массу придумал Ньютон, потому что ему нужно было как-то определить взаимодействия различных тел между собой в асболютном пространстве и абсолютном времени, которые еще более абстрактны как идеи. Ясного определения массы до сих пор не существует. Допустим, что это энергия. Зачем нам тогда вообще нужна идея массы, если можно просто пользоваться понятием энергии (тоже, кстати, весьма неопределённом)? Получается, что мы одно неизвестное определяем при помощи другого неизвестного. И убеждаем себя, что это космический закон, потому что он удачно описывает наблюдаемые явления.
А что, если энергия планеты зависит от ее орбитальной скорости и прочих орбитальных параметров не менее, чем от скорости света?
Потом, зачем нам нужна атмосфера на Марсе, подобная земной? Чтобы отправить туда наши тушки в консервной банке? Мы тут никак не можем поделить ресурсы планеты, так нам теперь нужно неперменно нашу войну перекинуть на Марс, чтобы еще и там устроить армагеддон? Почему жизнь обязательно должна иметь форму земной биологии? Может быть жизнь может существовать в какой-то другой форме?
Сам я тоже не люблю телевизор, и даже дома не имею, но иногда бывает, смотрю кое-какие программы. Вот на праздниках была весьма неплохая передача про Кольскую сверхглубокую скважину. В процессе её бурения, который занял несколько лет, все представления науки о земной коре были полностью пересмотрены. Оказалось, что гипотезы ученых вообще не имели под собой никакого реального основания. Там, где не ожидали найти воду, ее оказалось в изобилии, пердполагаемая температура и давление пласта оказались настолько несоответствующими фактам, что пришлось на ходу изобретать новое оборудование, чтобы продолжать бурение. И в науке это зачастую. Ученые часто с пеной у рта доказывают вещи, которые в реальности оказываются просто вымыслом. Почему? Да потому что нет философской базы, которая направляла бы научный поиск.
Я обязательно посмотрю Вашего Тейлора, кажется, я уже где-то на него натыкался. Как Вы считаете, я найду там ответы на озвученные мною вопросы? Я пробовал читать Хокинга. Признаюсь, его аргументация у меня вызывает ухмылку. Он настолько верит в тот образ, который сформировался у него в сознании, относительно БВ и т.п., что его совершенно не беспокоит, существует ли всё это на самом деле. Это подход религиозного фанатика. Он оперирует сложными конструкциями, при этом когда доходит дело до простых вещей, он вставляет какие-то нелепые откговорки, как, например, в вопросе о времени. Фактически, он не может дать определения времени, однако он постоянно опреирует этим термином. Это ключевой термин, хотя его точное значение не определено. Как можно верить подобным рассуждениям? Только в религиозном ключе, ИМХО, т.е. догматически.
Уважаемый Ingus,
Подскажите, пожалуйста, вот тут сформировался такой вопрос.
Если наблюдать движение Луны относительно Солнца, мы обнаружим самостоятельную солнечную (гелиоцентрическую) орбиту некоторого планетарного (+/-) тела, расположенную на сравнительно небольшом расстоянии от орбиты другого планетарного тела, большего по размерам.
Тут мы видим, что когда Луна находится на внутренней стороне орбиты Земли она "по идее" должна меньший путь (по хорде орбиты) проходить быстрее, чем на внешней стороне (по дуге, большей чем дуга орбиты), где расстояние должно быть больше. Иными словами, если мерять цикл Луны дугами солнечной орбиты Луны, то путь от певрой четверти до третьей должен быть фактически длиннее, чем, скажем, от новолуния до полнолуния и от полнолуния до новолуния, которые "как бы" средние по величине.
Однако, на более коротком внутреннем участке Луна еще и "отстаёт" от Земли, а на внешнем - "обгоняет" Землю.
Значит ли это, что гелиоцентрическая орбитальная скорость Луны имеет переменную величину? Или всё-таки она постоянна, как и у Земли?
Помогите рассчитать фактическую гелиоцентрическую (не геоцентрическую) орбитальную скорость Луны на участке от полнолуния до новолуния и от от первой четверти до третьей и опять до первой, одного и того же цикла, например, в области перигелия Земли, например, текущего. Или хотя бы подскажите методику, как это сделать.
Эллиптичностью мы пренебрегаем только в учебных целях!
Попробуйте понять Арнольда В.И. про эллиптичность и обратные квадраты.
Из приведенной статьи видно, что если "эллипс возвести в квадрат", то он останется эллипсом, только фокус его сместится в центр. Это красиво, но мне как неспециалисту не очевидна связь эллиптичности орбит с законом обратных квадратов: "В физике закон обратных квадратов — это закон, утверждающий, что значение некоторой физической величины в данной точке пространства обратно пропорционально квадрату расстояния от источника поля, которое характеризует эта физическая величина." (Википедия). Честно сказать, тут очень много дополнительных вводных, типа "отрицательной полной энергии" и проч. Моих скудных знаний в данной области, увы, не хватает.
Очень интересно. Изучаю. Часть вопросов осталась внизу.
Я посчитал среднюю скорость Луны за год. Получается 29844,3249. Если соотнести ее со средней орбитальной скоростью Земли, получается 1,002059. Значит в среднем Луна движется по гелиоцентрической орбите быстрее Земли. Правильно ли это? Как посчитать длину орбиты Луны? По идее, ее отношение к земной должно быть таким же, как и отношение скоростей, иначе Луна бы "улетела".
Намного ли усложнится задача, если учесть "вертикальную" компоненту орбиты Луны и сильно ли это повлияет на результат?
Я считаю, что вопрос о средней скорости Луны напрасно истоящает наши с Вами интеллектуальные ресурсы... Что Вы хотите найти или доказать в конечном счете?
И давайте все таки оставаться в рамках общепринятой терминологии. Орбита Луны не имеет вертикальной компоненты, как и горизонтальной. Реальная орбита Луны не круговая и даже не эллиптическая. Траектория Луны представляет собой сложную кривую, отдаленно напоминающую прецессирующий эллипс.
Я вижу орбиту Луны как гелиоцентрическую траекторию, начала циклов которой никогда не совпадают, т.е. это непрерывная линия, которая "обвита" вокруг орбиты земной. Прецессирующий эллипс - лучше, пожалуй, и не скажешь. Наверное, вообще все эллиптические орбиты так или иначе прецессируют, или это не так? Но гелиоцентрическая орбита Луны локализована и прецессирует еще и в диапазоне гелиоцентрической орбиты Земли, так ведь? От этого у нее орбитальная скорость примерно та же, прежде всего. Земную орбиту я вижу как непрерывную гелиоцентрическую линию, которая в целом укладывается в математическую модель эллипса. Хотя и у нее конец цикла не попадает точно в точку, откуда цикл началася, даже на очень большом диапазоне циклов. Т.е. орбита любой планеты это всегда своего рода прецессирующая эллиптическая спираль, "навитая" на солнечный стержень. Разве это не так?
Мы взяли плоскость орбиты Земли за базовую для своих расчетов. Для земных практических целей это безальтернативно. Но с гелиоцентрической точки зрения это не всегда корректно. Не может ли из этой некорректности возникунть интересная погрешность или, не дай бог, закономерность, которая в проекции на эклиптику нам просто не видна, как вы считаете, Иван Евгеньевич?
А по вопросу "вертикальной составляющей" орбиты Луны я имею в виду то, что она относительно эклиптики движется все время под углом, то выше, то ниже, ведь это тоже на скорости как-то сказывается? Там, конечно, наверное, незначительная поправка, и ею можно принебречь в выбранном масштабе, это понятно.
Говоря о прецессирующем эллипсе, я имел ввиду конечно же геоцентрическую орбиту Луны. Гелиоцентрическая орбита Луны выглядит иначе. Она по Вашему меткому замечанию обвита вокруг земной. И мы снова тонем в словах(( Я не могу ухватить, какую такую закономерность бог не дает Вам обнаружить? Вид расчетной траектории зависит от модели, принятой нами на вооружение. Если это задача двух тел, то решая дифур, полученный нами из второго закона Ньютона, мы увидим эллиптические траектории.
Если это задача трех тел, как в случае с Солнцем, Луной и Землей, дифур будет немного сложнее, но это будет все тот же второй закон Ньютона. Решая дифур, мы получим не эллипс, а змею навитую на эллипс. Чем больше тел мы будем брать в рассмотрение, тем хуже будет извиваться змея вокруг классического и простого эллипса. Все это описано в теории возмущенного кеплерова движения.
Иван Евгеньевич, я позволю себе предложить вам схемку, которую недавно нарисовал, только боюсь она не будет видна вся целиком. Ее проблема в том, что из соображений наглядности размер Земли и Луны увеличесны в миллион с лишним раз относительно длительности земного дня, которая дана в пропорции к земной орбите. Но зато она вполне наглядно демонстрирует, что Луна фактически не вращается вокруг Земли. Никаого эллипса лунной орбиты в реальности не существует, кроме гелиоцентрического.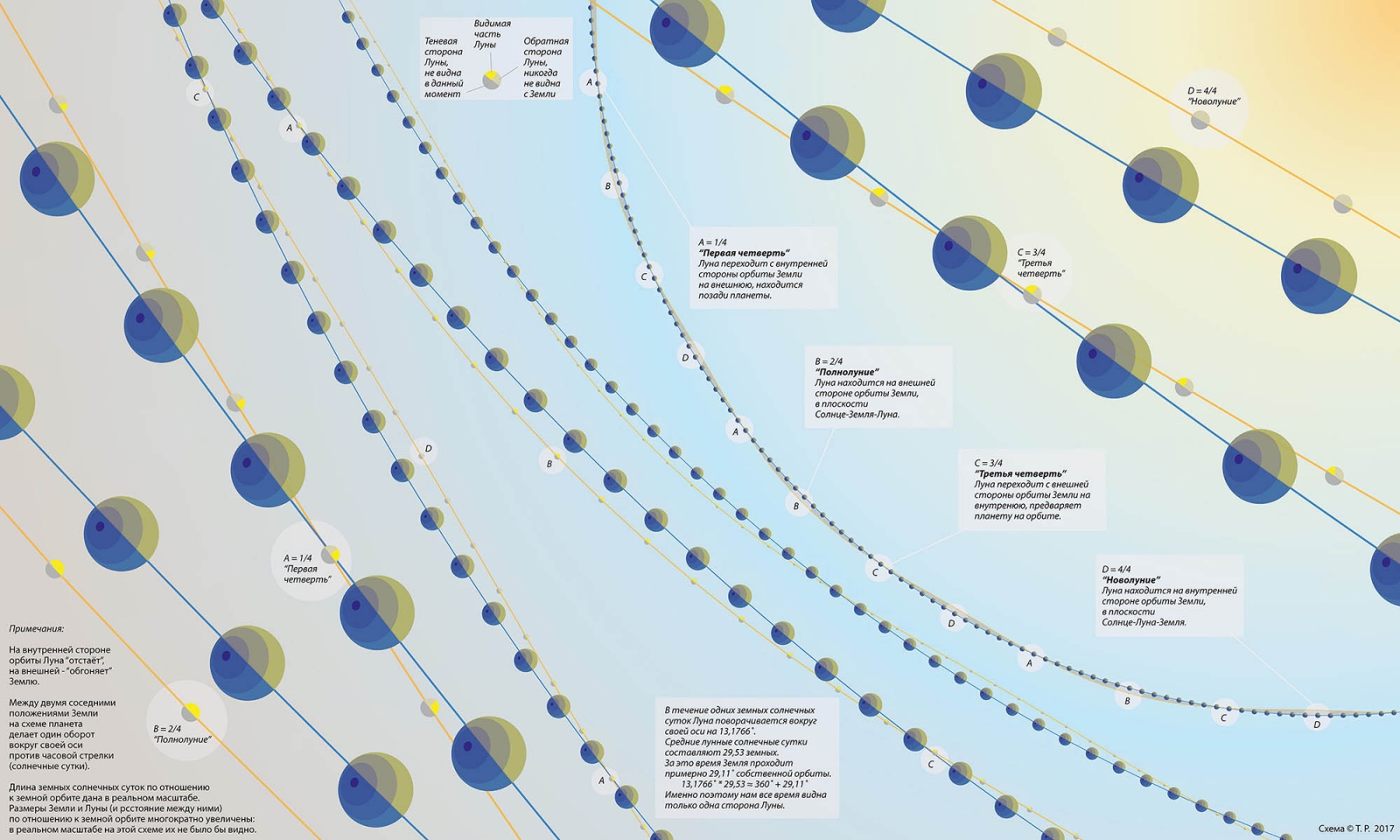
Красивая картинка! И да! Луна не вращается вокруг Земли, если смотреть на все это ангелом паря над Солнцем. Но стоит опуститься на грешную Землю, и Луна тотчас начинает вращаться вокруг Земли... Если Вы, к примеру, вальсируете с дамой в вагоне ресторане движущегося поезда, то очевидно для Вас и дамы Вы кружитесь. Она вращается вокруг Вас, а Вы вокруг нее. Я же, наблюдая издалека в подзорную трубу, увижу Вас несущимися со страшной скоростью наперегонки, попеременно обгоняя друг друга... и никакого вальса...
Отрицая вращение Луны вокруг Земли, Вы отрицаете притяжение Земли и Луны. А оно есть) Две металлические болванки, между которыми притяжение ничтожно, Вы никогда не заставите двигаться вокруг Солнца теми же замысловатыми путями, что у Земли с Луной.
Итак, уважаемый, Тимофей Александрович, я спрошу Вас как инквизитор от астрономии, вращается ли Луна вокруг Земли?)
Зачем Вы истощате свой ум столь бесполезной работой?
Уважаемый Иван Евгеньевич! Как раз притяжение я не отрицаю, оно, очевидно, существует. Надо полагать, что именно притяжением обусловлена неравномерность скорости, которую с Вашей помощью мы выше установили.
Если Луна вращается вокруг Земли, давайте определим координаты эллиптической орбиты Луны относительно эклиптики. Можете указать ее (эллиптическую орбиту) на схеме? Или вы не согласны с этой схемой?
Вот про ИСЗ я бы не сказал, что у них есть своя гелиоцентрическая орбита - у них есть гелиоцентрическая траектория, да, но при этом они полностью находится в поле Земли, под ее "колпаком" - плоть от плоти; Земля - это поезд, а ИСЗ - пассажиры.
Геоцентрика очень крепко держит нас за горло. Потому что она соответствует эмпирике, мы к ней привыкли, у нас все модели под нее "заточены". Но она не соответсвтует фактам. И это очень мощное противоречие. Если мы хотим по-настоящему осваивать космос, необходим полный переход на гелиоцентрику, таков мой основной тезис. Мне кажется, при современном уровне знаний, не должно составить большого труда построить гелиоцентрическую математическую модель СС.
Я очень благодарен Вам, что Вы находите возможность дискутировать со мной, но мне бы не хотелось истощать благосклонности Вашего внимания, поэтому предлагаю оставить этот спор, и попробуем вернуться к практическим вопросам, т.е. к расчетам.
Я понимаю, что Вас не свернуть с пути, и Вы намерены расправиться с "геоцентрикой" окончательно. Но это все пустое...
И что такое "координаты эллиптической орбиты Луны относительно эклиптики"? Дичь. Пусть $\overline{R}$ - радиус-вектор центра Земли в гелиоцентрической системе отсчета, $\overline{\rho}$ - радиус-вектор центра Луны в гелиоцентрической системе отсчета (как функция времени ессно)
Тогда $\overline{r}= \overline{\rho}-\overline{R}$ - траектория, она же орбита Луны в геоцентрической системе.
Не могли бы Вы более внятно объяснить, что именно не соответсвует фактам (каким?) и в чем мощное противоречие, т.е. что чему противоречит?
Если оба исходных вектора суть функции времени, то я не понимаю, каким образом результирующий вектор дает эллипс. Чтобы орбита Луны превратилась в эллипс, движением Земли во времени нужно принебречь.
Фактом является движение Земли по солнечной орбите. Этому факту противоречит геоцентрическая модель мира.
А Вы постройте результирующий вектор в полярных координатах...Как фунцию времени ессно. И все поймете, надеюсь..
Фактом является и движение Солнца по галактической орбите. Что Вы понимаете под геоцентрической моделью мира? Это важно.
В околоземных расчетах нет смыла лезть в гелиоцентрическую систему, и мы с успехом можем использовать геоцентрическую математическую модель, не модель мира, прошу заметить. Для Луны это не прокатывает. А вот для расчета прецессии и нутации земной оси - за милую душу.
Что Вы кстати читали у Коперника? Там ему в предисловии один товарищ удружил - написал, мол гелиоцентрический подход, это просто математический прием для удобства расчетов, видимо, чтоб католическую церковь не провоцировать на разжигание костра.
Так и я Вам скажу, геоцентрический подход, это всего лишь математический прием, упрощающий решение ряда задач и не более.
Еще замечу, что Птолемей считал точнее Коперника... Угадайте почему...
А по поводу геоцентрической модели мира я имею в виду птолемеевскую модель со всеми шаблонами, которые нам от нее достались. Эклиптика, например; или небесный экватор, движение светил по небесной сфере и т.п. вещи; хотя сегодня они низведены с уровня "системы" на уровень "модели", тем не менее в восприятии небесных процессов они играют подчас определяющую роль. Птолемей воспринимал эти вещи буквально, а мы "знаем" что это не так, но отношение наше практически не поменялось. Я бы сказал, образно выражаясь, что в нашем распоряжении имеется глобус, но мы продолжаем использовать карту, потому что это нам удобнее. Кстати, Птолемей не считал точнее Коперника. В самом предисловии Коперник пишет, что вопрос об "исправлении церковного календаря" так и не решен, ни Птолемеем, ни его последователями, и именно эта научная проблема подвигла его к собственным изысканиям. То, что "Альмагест" инкорпорирует в себя несколько тысяч лет астрономических наблюдений, конечно, придает ему огромный вес в плане точности расчетов. Однако, уже Аристарх Самосский (работ которого Коперник, вдимо, не знал) предполагал движение Земли вокруг Солнца, и его календарная математика оказалась в итоге точнее.
Коперника я пролистал "О вращениях небесных сфер...", это интересный труд, но он только положил начало. Надо заметить, что труд этот был полностью признан католической церковью, папа Павел Ш, к которому он обращается в предисловии, был человеком просвещенным и относился к астрономии с пониманием. Жечь Коперника никто не собирался, тем более, что книга вышла в год его смерти. Намного большего интереса, на мой взгляд, заслуживают "Диалоги" Галилея. К этому времени, после еретических отступлений Бруно, ситуация накалилась. Кстати, Бруно сожгли вовсе не за коперниканство, а, скажем так, за нео-языческий пифагореизм. В контексте католичества он был нераскаивающимся (до костра его продеражали лет семь в застенках инквизиции, где требовали одного - вернуться в лоно церкви) еретиком. Он пытался использовать идеи Коперника для пропаганды своих взглядов, чем скорее "навредил" последнему.
Галилею пришлось попотеть больше других, но его "Диалог", я считаю, блестящим примером здравого смысла. Чего стоит одна только история о том, как бросают камень с мачты движущегося корабля.
Вообще говоря, я, вслед за Коперником, Галилеем, Кеплером, считаю астрономию царицей наук. Тот факт, что перподавание астрономии вернули в шклоу, на мой взгляд, очень хороший знак. Единственно, мне кажется, что астрономию нужно преподавать с первого класса как минимум час в неделю, с обязательным наблюдением звездного неба, с изучением всех упомянутых выше трудов и даже биографий.
Если бы не Ретик, неизвестно, опубликовался бы Коперник сам... Не сразу, но церковь наложила запрет. Вопреки устоявшемуся мнению, сама книга Коперника «De Revolutionibus Orbium Coelestium» была формально запрещена инквизицией лишь на 4 года, однако подверглась цензуре. В 1616 году она была внесена в римский «Индекс запрещённых книг» с пометкой «до исправления»; перечень цензурных поправок был обнародован в 1620 году. Книга «De revolutionibus» стала первым в истории чисто научным трудом, попавшим в «Индекс»; до неё Ватикан преследовал только религиозные или оккультистские сочинения. До сожжения книги оставался один шаг.
С современной точки зрения, модель Коперника недостаточно радикальна. Все орбиты в ней круговые, движение по ним равномерное, так что для согласования с реальными наблюдениями пришлось сохранить искусственные птолемеевы эпициклы — правда, их стало несколько меньше. Однако теория Коперника не привела к существенному увеличению точности расчёта движения планет: реальное движение планет не является ни круговым, ни равномерным. Наихудшее согласие с наблюдениями модель Коперника давала для планет с большим эксцентриситетом (Меркурий, Марс, Сатурн)
Полярная система координат двухмерная. В ней, понятное дело, все сойдётся. Стоит сделать шаг к сферической системе, как все тут же разваливается. Я, разумеется, не спорю, что можно найти некоторую плоскость, проекция на которую даст эллипс лунной орбиты, но в реальности этой плоскости не существует.
Насколько движение Солнца по галактической орбите является фактом, никому не известно. Оно с тем же успехом может вращаться вокруг каких-то иных центров, которые в свою очередь могут двигаться по галактическим орбитам. Этот спор я считаю в настоящий исторический момент бесперспективным. Вы, видимо, хотите сказать, что можно было бы с тем же успехом сразу переходить на галактические координаты, и вот с этим я полностью согласен. Тут я бы сделал только одно замечание, по "галактической орбите" движется не Солнце и планеты как некие изолированные космические тела, а вся солнечная система как целое. Это важно. В случае с Луной иерархия иная - она как раз имеет собственное движение в контексте СС.
Мы осваиваем СС именно с целью последующего освоения галактической. Но для этого пока у нас нет ни инструментов, ни моделей, ни даже данных. А вот освоить гелиоцентрику нам вполне по силам.
Про околоземные расчеты я и не спорю, выше я уже говорил об ИСЗ. Геоцентрическая модель однозначно имеет свои преимущества именно как модель. Но как вы совершенно точно выразились, уже для Луны это не прокатывает.
Так сделайте это шаг! От полярной к сферической. Добавьте пару углов Эйлера. Ничто не развалится. Проекция Лунной геоцентрической орбиты на плоскость орбиты Земли это прецессирующий эллипс, на манер траектории сферического маятника на вращающейся платформе, типа маятника Фуко.
Иван Евгеньевич, Вы лучше посоветуйте мне какой-нибудь задачник по углам Эйлера. Это, если я правильно понимаю, как раз касается вычисления точек равноденствия на Марсе.
Посмотрите в моих статьях на этом сайте, может там что-то полезное найдте по углам.
Уважаемый Ingus, (простите, а как Ваше имя-отчество?), я вынужден прервать наш интереснейший диалог до понедельника, когда надеюсь с вашей помощью узнать еще пару астрономических секретов. Надеюсь, я не слишком Вас утомляю?
У меня помимо лунной темы есть еще кое-какие вопросы по небесной механике, могу ли я расчитывать на вашу помощь?
Уважаемый Stupa, в миру я Иван Евгеньевич. А Вы? И да. Мне приятно быть полезным и отвечать на вопросы истинного ценителя вечности. Ибо только таковым интересна Луна и небесная механика, в которой я кое-что понимаю.
А я Тимофей Александрович, несмотря на псевдоним. Вечность - это наше все. С нетерпением жду задачи про ускорение.
А еще меня интересует вот какой вопрос. Как известно, есть 5 основных систем координат, но между ними нет ни одной гелиоцентрической, где центром координат был бы центр Солнца, а базовой плоскостью - плоскость солнечного экватора. Говорят, что, мол, "так удобнее", а на мой взгляд - это геоцентрический анахронизм; даже термины, которыми мы пользуемся, "небесная сфера" по которой происходит "видимое движение Солнца", все это пережитки птолемеевой эпохи, которые сегодня, 500 лет спустя после Коперника, в эпоху "покорения" космоса кажутся несколько условными. Как можно даже пытаться жить на Марсе относительно земной эклиптики? Ведь там своя "эклиптика"! Так вот по поводу Марса: как мне рассчитать угол между направлением на перигелий и на точку зимнего солнцестояния (или ТВР) относительно плоскости орбиты Марса? Нигде не смог найти методики. Но может быть, чтобы не путать ветки обсуждения, попытаться обсудить этот вопрос в другом месте?
Тимофей Александрович, а Вы смотрели программу Stellarium? Может там можно марсинское небо увидеть с его эклиптикой и экватором? Проверьте...
Stellarium чудесная вещь. Но дело не в марсианском небе. Я пытаюсь составить схему орбиты Марса в марсианских координатах, безотносительно Земли. Получается, что кеплеровы элементы орбиты привязаны всякий раз к земным координатам, но если мы на Марсе, предположим, то зачем нам это? Вот и Стеллариум все время дает координаты к земной эклиптике, или я ошибаюсь? Если вы мне подскажите, какие данные надо взять из стеллариума и как их соотнести, я буду очень признателен. Я с ним практически еще не очень освоился.
Почему-то у меня в стеллариуме с какой планеты не смотри, горизонт все время земной, с травкой, с домиками, и атмосфера земная, та же плотность воздуха. Смотришь с Юпитера, а Солнце там как на Земле, большое, желтое. Или с Каллисто.
Вы не поверите, но я спустя 500 лет после Коперника решаю задачи на прецессию и нутацию Земли, считая, что движется Солнце. Это действительно удобнее!! Попробуйте.
Так, и я о том же. Все доподлинно знают, что Солнце находится в центре системы, а не Земля, но до сих пор у нас по жизни оно "всходит" и "заходит", и мы часто буквально воспринимаем эти слова. Основная масса людей, и даже многие специалисты, все равно по умолчанию живут в геоцентрической системе, хотя всем теоретически известно, что это не так. Как Птолемей положил мерять углы на небесной сфере, так мы и делаем. Хотя факт в том, что нет вообще никакой небесной сферы. Просто нам так удобнее, да и другой системы отсчета у нас реально же нет, только земная.
Говорят, что у нас нет практической необходимости. Какая нам разница, какой там на Марсе календарь, какие там сезоны, мы же тут. Однако, оказывется, даже это вопрос не праздный, и НАСА этим занималось, потому что даже для марсохода удобно иметь местные координаты времени, а не только земные, чтобы отслеживать периоды освещенности батарей, например.
Вообще меня занимает вопрос календарных систем СС. Вы, конечно же знаете про математику Венеры, 25/13 и 12/13? На мой взгляд это поразительно красиво математически. Земная привязка этой красоте, ИМХО, порой несколько мешает.
Тимофей Александрович, вот Вам задача про ускорение: найти вектор ускорения Луны и оценить трансверсальную компоненту этого ускорения в зависимости от фазы Луны.
Уважаемый Иван Евгеньевич, давайте оставим ненужные споры и по возможности перейдем к расчетам. Подскажите, как практически подойти к решению поставленной Вами задачи?
Мы с Вам нашли скорость Луны в декартовых координатах $\dot x$, $\dot y$. Найдем теперь $\ddot x$ и $\ddot y$. Это будут компоненты ускорения. Построим вектор ускорения в ключевых точках - сизигиях и квадратурах.
Для скорости мы использовали формулу:
$v(t)=(\dot x^{2} + \dot y^{2})^{1/2}$
а какова итоговая формула для ускорения?
Она аналогична. Только на этот раз я просил показать вектор. Не модуль.
Поставил MatLab R2014b. Надеюсь, это поможет. Потому что я не очень понимаю, как "показать вектор". Прошу подсказку.
Ну хотя бы так..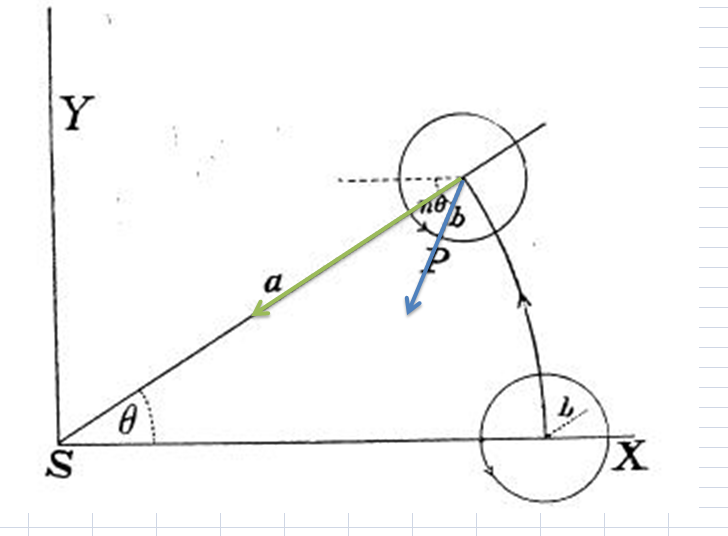
Если я правильно понимаю смысл задачи,
в новолуние $n\theta = n\omega t = 0^{\circ}$
в первой четверти $n\theta = n\omega t = 90^{\circ}$
в полнолуние $n\theta = n\omega t = 180^{\circ}$
в третьей четверти $n\theta = n\omega t = 270^{\circ}$
Угол $\theta= \omega t$ в первой четверти будет равен $90^{\circ}/n$ и т.д.
Теперь яснее. Итак, вторые производные:
$\ddot x = bn^{2}\omega ^{2}cos(n\omega t)-a\omega ^{2}cos(\omega t)$
Вот, побалуйтесь Вольфрамом, если интересно. Это наша с Вами скорость Луны.
Мне удалось построить график скорости в Матлабе. Прошу, помогите с практическими указаниями, как дальше действовать в отношении ускорения.
Нужно освоить параметрическое представление функции. По одной оси $\ddot x(t)$ по другой $\ddot y(t)$
А в итоге что мы должны получить, график? У меня получился такой:
Красиво. Но извлечь полезную информацию из этого цветочка достаточно сложно. Эту витую спираль очерчивает конец вектора абсолютного ускорения Луны. Мне бы хотелось увидеть этот вектор в ключевых точках - сизигиях и квадратурах, причем на фоне радиус-векторов Солнце-Земля и Луна-Земля.
А почему не Солнце-Луна и Земля-Луна? Мы же хотим оценть влияние Солнца и Земли на Луну?
Честно сказать, не знаю, с какой стороны подойти к этой задаче. Подставить в формулы углы и получить координаты? Но это будет пара координат, а тут, как я понимаю, должно быть минимум две пары, раз векторов два.
Я придумал подсказку... Запишите закон всемирного тяготения в векторном виде...
Я понимаю, что по сути расстояния a и b мы можем рассматривать как векторы. В новолуние они будут противоположны по направлению, т.е. получится (a-b), a в полнолуние наоборот, оба будут направлены в сторону Солнца, (a+b). В этих точках ускорение будет достигать экстремумов. А в первой и третьей четвертях они будут перпендикулярны, и в этих точках ускорение меняет знак. Я только не знаю, как это записать в виде формул. Практического навыка не хватает.
Я хочу сделать одну оговорку. Мы с Вами записали траекторию Луны, не решая дифференциального уравнения. Эмпирически. В действительности, если подставить наши значения $а$, $b$, $n$ в соответсвующие ДУ, мы получим несколько иную траекторию.
Попутно возникает вопрос, как подобрать параметры $а$, $b$, $n$, чтобы полученная решением ДУ геоцентрическая траектория Луны была окружностью.
Векторное уравнение, которое я просил написать, выглядит так:
$\overline a_m=\frac{G M_s}{\rho^3} \overline \rho+\frac{G M_e}{r^3}\overline r$
Сможете его расшифровать?
Вектор в нашем случае это пара координат. Для того, чтобы их получить нам не придется решать ДУ, потому, что мы уже эмпирическим путем нашли траекторию Луны.
Распишете тройку векторов $\overline a_m, \overline \rho, \overline r$ в координатах?
Я хочу сделать одну оговорку. Мы с Вами записали траекторию Луны, не решая дифференциального уравнения. Эмпирически. В действительности, если подставить наши значения $а$, $b$, $n$ в соответсвующие ДУ, мы получим несколько иную траекторию.
А когда мы брали производные, это не было решением ДУ? Каково же тогда исходное уравнение?
Попутно возникает вопрос, как подобрать параметры $а$, $b$, $n$, чтобы полученная решением ДУ геоцентрическая траектория Луны была окружностью.
Геоцентрическая? Мне кажется, у геоцентрической орбиты тут нет шансов. Если из этих параметров нужно сделать окружностью гелиоцентрическую орбиту, то мне кажется, $b$ и $n$ должны быть равны 1.
Векторное уравнение, которое я просил написать, выглядит так:
$\overline a_m=\frac{G M_s}{\rho^3} \overline \rho+\frac{G M_e}{r^3}\overline r$
Сможете его расшифровать?
Расшифоровать.
$\overline a_m$ - надо полагать, искомое укорение. $M_s$ - масса Солнца. $M_e$ - масса Земли. $\overline \rho$ - радиус-вектор Солнце-Земля, $\overline r$ - радиус-вектор Земля-Луна. Так?
Но разве в числителе не должно стоять произведение масс?
$\overline a_m=\frac{G M_s M_m}{\rho^3} \overline \rho+\frac{G M_e M_m}{r^3}\overline r$
Если так, то не понятно, где же тут масса Луны? Разве она не нужна нам здесь? Вообще, мне представляется, что по сути нам нужно два других вектора, вектор Земля-Луна и вектор Солнце-Луна. Если мы рассматриваем гелиоцентрическую орбиту Луны, а не системы "Земля-Луна".
И еще. Честно сказать, я до последнего момента верил, что мы сможем обойтись тут без G и масс. Хотя и не понятно, как в таком случае можно оценить влияние Земли и Солнца. Как вы считаете, можно ли это GM как-нибудь вынести за скобки?
Вектор в нашем случае это пара координат. Для того, чтобы их получить нам не придется решать ДУ, потому, что мы уже эмпирическим путем нашли траекторию Луны.
Распишете тройку векторов $\overline a_m, \overline \rho, \overline r$ в координатах?
Если с расшифровкой я не ошибся, то по всей вероятности координаты $\overline \rho$ должны быть $(x=a*cos\theta, y=a*sin\theta)$. Для $\overline r - (x=b*n^2*cos(n\theta), y=b*n^2*sin(n\theta$)), а для $\overline a_m$ по всей видимости сумма этих двух, т.е. по сути та самая вторая производная, которую мы брали.
$\overline \rho=(x,y)$
$\overline a_{m-s}=(\frac{G M_s}{(x^2+y^2)^{3/2}} x, \frac{G M_s}{(x^2+y^2)^{3/2} }y)$
$\overline r=??$
$\overline a_{m-e}=??$
Продолжите...
$\overline \rho=(x,y)$
$\overline a_{m-s}=(\frac{G M_s}{(x^2+y^2)^{3/2}} x, \frac{G M_s}{(x^2+y^2)^{3/2} }y)$
$\overline r=??$
$\overline a_{m-e}=??$
Продолжите...
Так?
$\overline r=(x_1,y_1)$
$\overline a_{m-e}=(\frac{G M_e}{(x_1^2+y_1^2)^{3/2}} x_1, \frac{G M_e}{(x_1^2+y_1^2)^{3/2} }y_1)$
Хитро! А я не знал, что так можно... Т.е. в знаменателе он получается "по модулю"?
Круто. А $x_1$ и $y_1$ это что? Чему равно?
Это координаты. Такие же, как х и у.
Это координаты Луны относительно Земли... Через них сила притяжения Луны Землей и ускорение считаются. Так чему же они равны?
Боюсь ошибиться, но может быть
$x_1=b*n^2*cos(n\theta),$
$y_1=b*n^2*sin(n\theta)$
?
Вы шутите))
$x_1=x-a \cos\theta$
А как же нам тогда определить сизигии и квадратуры, если ни b, ни n у нас не фигурируют в формулах? И зачем мы брали вторые производные? И как нанести на грфик GM?
Нет. Когда мы брали производные, мы шли снизу вверх… от траектории к силам через ускорения. Решая ДУ, мы идем сверху вниз… от сил к траектории.
Орбита Земли в нашей модели круговая. Подбирая параметры, мы и Луну можем заставить летать по кругу около Земли, в геоцентрической СО.
Да. Нам нужны вектора Солнце-Луна и Земля-Луна. Именно их я и выписал.
Вы размерности то проверяйте иногда! Если в числителе произведение масс, то это уже сила, а не ускорение.
Орбита Земли в нашей модели круговая. Подбирая параметры, мы и Луну можем заставить летать по кругу около Земли, в геоцентрической СО.
Для этого достаточно, чтобы b было постоянным. Ну, и угол поворота. Разве в представленной модели геоцентрическая орбита Луны и так уже не круговая?
Если бы Луна за одни земные сутки успевала бы сделать 10-20-100 оборотов вокруг Земли, наверное, имело бы смыл говорить о геоцентрической орбите Луны. А так... Неужели мы без нее никак не обойдёмся? Или, зачем нам эти данные? Они сильно упрощают расчёты?
Я все пытаюсь Вам втолковать, что решая систему ДУ для движения Луны в поле тяготения Солнца и Земли одновременно очень трудно подобрать параметры, чтобы Луна двигалась точно по окружности около Земли, как в нашей эмпирической модели...
И потом, насколько я понимаю, Луна фактически не движется вокруг Земли по окружности даже в контексте геоцентрической модели - принято называть эту орбиту эллиптической. Зачем же нам нужно "истощать наш с Вами интеллектуальный потенциал" и выдумывать то, чего в природе не существует?
"Чтобы продать что-нибудь ненужное, нужно сначала купить что-нибудь ненужное, а у нас денег нет". Чтобы понять что-либо, нужно отказаться от мелочей, типа эллиптичности, упростить модель так сказать.
Согласен! Но вдруг эллиптичность - это не мелочь, а неизбежное следствие некоторого закона (для нас пока не очевидного), пренебрегая которым мы утрачиваем связь с реальностью и переходим всецело в сферу умозрительного?
Эллиптичность следствие очевидного закона обратных квадратов. Но для понимания общей картины мы ею пренебрегаем. Вы же наверное раскладывали функцию в ряд Фурье? Можно в первом приближении ограничиться константой и отбросить все гармоники.. Хотим точнее знать? Добавляем первую гармонику... Потом вторую.. и так далее до бесконечности, приближаясь к идеалу...
Не очень понимаю, в чем связь эллиптичности и закона обратных квадратов?
Однако, эллиптичностью мы пренебрегаем далеко не всегда, например, в случае Меркурия ею сложно пренебречь.
\\
лаконично
Пост я перенес выше. В начало.
Хм. Понимаете, Иван Евгеньевич, Ваша изначальная статья привлекла меня как неспециалиста, поскольку тут было предложено красивое решение для гелиоцентрической орбиты Луны без учета GM. Когда мы с вами посчитали скорость теми же методами, как Вы говорите, эмпирическими, всё это стало ещё интереснее, поскольку мы тут имеем дело исключительно с гелиоцентрической орбитой. Единственное допущение, которое мы делаем, это то, что расстояния a и b постоянны. Вместо а мы можем подставить реальное значение радиус-вектора, для b мы также можем взять некоторую переменную величину - фактическое расстояние. Ведь оно же нам известно?
Лично для меня является фактом, что никакой геоцентрической орбиты Луны не существует в природе, она существует только в нашем воображении. Геоцентрическая орбита нужна нам как математическая модель для решения ряда прикладных задач. Поэтому, очевидно, подбор параметров вырастает в сложную задачу, потому что мы хотим умозрительную модель привязать к реальному движению, не имея при этом ясного понимания того, как и почему данное движение (орбитальное, осевое) вообще происходит. Не знаю, готовы ли вы согласиться, что помимо ряда неподтверждаемых гипотез мы ничего не знаем ни о происхождении Земли и Луны, ни о том, как и почему они движутся. Зачем нам озадачиваться подбором параметров, если никакой реальной эмприрке это всё равно не соответствует? Не лучше ли рассматривать реальное движение и в нём пытаться обнаружить какие-нибудь закономерности.
Когда мы хотим посчитать, как действуют на Луну массы Солнца и Земли, мы приходим, если я првильно понимаю, к задаче о взаимном движении трех тел. Мне сдаётся, что эта задача в общем случае не имеет решения. И конечно, без учета масс и расстояний, т.е. без батюшки Ньютона тут и вовсе делать нечего. Однако, позвольте спросить, можем ли мы сделать еще какие-то шаги в исследовании гелиоцентрической орбиты луны без учёта масс Солнца, Земли и Луны? Например, можно ли рассмотреть движение Луны по своей орбие (гелиоцентрической) с точки зрения второго закона Кеплера? Ведь если небесное тело движется по гелиоцентрической орбите, то этот закон для такого тела должен выполняться?
Не собирался я заниматься подбором параметров.
Я Вам больше скажу, гелиоцентрической орбиты Луны тоже не существует... Солнце же не покоится... Все движется. И все зависит от того, где находится наблюдатель. Вы где находиться предпочитаете? На Солнце? Тогда да, орбита Луны похожа на орбиту Земли. А я вот в центре галактики нашей был. Как посмотришь оттуда, Луна такие кренделя выписывает! А по возвращении домой в окно глянешь - Луна вокруг Земли так и ходит...
У нас нет точного знания о том, как образовалась система Земля-Луна, только несколько гипотез.
Задача трех тел в случае С-З-Л упрощается, ибо Солнце в силу превосходства его массы можно остановить.
Хотите Кеплера понять? Второй закон выводится из сохранения момента импульса? Запишите момент импульса Луны и скажите сохраняется он или нет.
Я Вам больше скажу, гелиоцентрической орбиты Луны тоже не существует... Солнце же не покоится... Все движется. И все зависит от того, где находится наблюдатель. Вы где находиться предпочитаете? На Солнце? Тогда да, орбита Луны похожа на орбиту Земли. А я вот в центре галактики нашей был. Как посмотришь оттуда, Луна такие кренделя выписывает! А по возвращении домой в окно глянешь - Луна вокруг Земли так и ходит...
Это так лишь до определённой степени. Предположим, что Солнце не покоится и совершает относительно центра галактики какое-то движение. Понятно, что с учётом этого движения реальные траектории тел, составляющих СС, также "разворачиваются" из эллиптических в "витые" линии. Однако, есть большая разница между взаимным движением Земли и Луны относительно Солнца, и всех троих относительно ЦГ. СС - это целостный организм, который имеет некоторую границу. Все движения в системе "отделены" от того, что происходит за ее пределами. Пример с поездом, который вы выше приводили, тут более уместен, чем в случае с Луной и Землёй. Все объекты СС своим источником имеют Солнце, чего не скажешь о системе Земля-Луна. Из центра галактики ни Земли, ни Луны, ни даже Юпитера не видно - вся сия суть лишь "параметры" звёздной жизни Солнца. Их отдельные траектории в галактической перспективе теряют смысл.
И кроме того, движение СС относительно ЦГ есть такая же недоказываемая гипотеза, как и проблема возникновения Земли, Луны, да и самого Солнца. Зато движение планетарных тел по эллиптическим орбитам открыто нам в нашем опыте, и мы можем применить к этому движению математический метод для обнаружения закономерностей данного движения.
Хотите Кеплера понять? Второй закон выводится из сохранения момента импульса? Запишите момент импульса Луны и скажите сохраняется он или нет.
Тут мне опять не хватает навыка с формулами, но рассуждаю я так. Если взять $L=r*p=r*mv$, то тут масса постоянная, а скорость $v$ и радиус $r$ величины переменные, причем чем меньше $r$, тем меньше и $v$ и наоборот. Исходя из этих соображений должно получатся, что момент импульса для гелиоцентрической Луны не сохраняется. Так?
Вот если бы на внешней стороне орбиты Луна двигалась медленнее и отставала от Земли, а на внетренней - наоборот, тогда, мне кажется, закон Кеплера бы срабатывал. По идее ведь так и должно быть - чем ближе к Солнцу, тем выше орбитальная скорость. Но у Луны почему-то не так. Почему?
Вы правы, это опечатка, а на самом деле это : Солнце-Луна и Земля-Луна.
Вы ждете подсказку? Сами не хотите придумать способ?
вторая строчка не правильно
Ну конечно!
$\ddot x = bn^{2}\omega ^{2}cos(n\omega t)-a\omega ^{2}cos(\omega t)$
Вот, именно это самое интеерсное. Но если честно, я не понимаю, с какой стороны к этому подойти. В экселе я построил таблицу, где делю текущее показание скорости на предыдущее и смотрю динамику. А вот как в векторной форме это представить, пока не постиг. Почему и обращаюсь.
Пора Вам освоить MathCad или MathLab
Уважаемый Stupa!
Благодарю за внимание, проявленное к моему скромному труду! Слова порой нас вводят в заблуждение, формулы же беспристрастны. В статье привдена зависимость гелиоцентрических координат Луны от углов. Положим угловые скорости движения Земли и Луны постоянными и продифференцируем координаты по времени. В итоге мы получим гелиоцентрическую скорость Луны в любой момент времени. Давайте график ее построим, что ли.
По поводу слов и формул полностью согласен. Давате построим график. Только как? Мне, как неспециалисту, не очень понятно, с чего начать.
По поводу вашего скромного труда хочу заметить, что в интернете нигде больше не нашел ни одной статьи по вопросу гелиоцентрической орбиты Луны (в русском сегменте, у буржуев не искал). А мне кажется, этот факт заслуживает более пристального внимания. Ведь это в итоге касается всех вообще спутников всех планет.
А Вы до какой степени неспециалист? Производные брать умеете? Писать формулы LaTex можете?
Нужно взять производную от $x=a\cos\theta-b\cos n\theta$
А нельзя посчитать реальную скорость Луны в км/с через истинную аномалию Земли?
Насколько я помню из школьного курса математики, производная от указанной вами функции должна быть: x'= b*n*sin nθ - a*sinθ.
Честно сказать, давненько я "не брал в руки шашек"... Что такое LaTex я не знаю :( Но могу посчитать в экселе.Выше вы считаете n=13, а дробное значение, т.е. 12,37, тут нельзя подставить?
Ну потрудитесь, уж, что тут сложного? Два значка доллара, а между ними выражение... И все у нас с Вами красиво получится:
Как я и сказал, положим угловую скорость обращения Земли по орбите постоянной и равной $\Omega$. Тогда $\theta=\Omega t$. Следовательно,
$\dot{x}=b n \Omega \sin n \Omega t - a \Omega \sin \Omega t$
Так?
А теперь сделайте для $\dot{y}$ то же самое...
Поставил texmaker, разберусь с ним и вернусь к Вам на консультацию.
Вот здесь очень просто можно научиться писать формулы http://www.codecogs.com/eqneditor
Формулы кажется такие должны быть, но как из них график построить в этом latex пока не понимаю.
Замечательно! Быстро Вы освоились! Вот только забыли точку поставить над $x$ и $y$. \dot x=$\dot x$
Теперь возведите обе компоненты скорости в квадрат и сложите.
В смысле, x'2+y'2?
А в чем смысл?
Ну мы же скорость ищем? Луны. Гелиоцентрическую.
так?
Боюсь, что не так... Как Вы получили удвоение? Давайте распишем здесь квадраты компонент:
$\dot x ^2=b^2n^2\omega^2\sin^2 n\omega t+a^2\omega^2\sin^2\omega t-2abn\omega^2\sin\omega t\sin n\omega t$
Понял про значки доллара.
Итак:
$\dot x^{2} + \dot y^{2} =b^{2}n^{2}\omega ^{2}+a^{2}\omega ^{2}-4abn\omega ^{2} cos(\omega t-n\omega t)$
Короче, итог, кажется, такой:
у меня почему-то код формул не получается вставить, в предпросмотре он остается кодом, только картинкой получается
А что за браузер у Вас?
так?
Я в четверке сомневаюсь... и не видите ли Вы возможность свернуть выражение в скобках?
$\dot x^{2} + \dot y^{2} =b^{2}n^{2}\omega ^{2}+a^{2}\omega ^{2}-2abn\omega ^{2} cos(\omega t-n\omega t)$
ну да, с 4 погорячился
Какие скобки свернуть, в косинусе?
Что можете сказать о графике?
Воот! Уже лучше. Это уже можно построить...
И да, простите, а какова все же формула скорсоти v(t)? Прямо так:
$v(t)=\dot x^{2} + \dot y^{2} =b^{2}n^{2}\omega ^{2}+a^{2}\omega ^{2}-4abn\omega ^{2} cos(\omega t-n\omega t)$ ?
Конечно нет!
$v^2(t)=\dot x^{2} + \dot y^{2} =b^{2}n^{2}\omega ^{2}+a^{2}\omega ^{2}-4abn\omega ^{2} cos(\omega t-n\omega t)$
А, ну да, понятно.
А чему равны переменные, в частности ω
С размерностями нужно аккуратнее... Первое правило. Расстояние всегда метры, время - секунды, масса - килограммы. Тогда не запутаетесь. $\omega$ это $2\pi$ деленное на продолжительность года в секундах.
А n в таком случае чему равно? 12,369?
И a - большая полуось в метрах? А b ?
Похоже, что скорость Луны на гелиоцентричекой орбите есть величина переменная. Единицы измерения тут не очень ясны, но по всей вероятности, она должна быть в диапазоне 28,7-30,7 км/с. Причем в начале периода она минимальная, в середине периода - достигает максимума и снова доходит до минимума к смене периодов. Что тут мы считаем началом периода? Новолуние?
Вопрос вот в чем: откуда она "знает", что ей нужно то притормаживать, то разгоняться?
Да. Новолуние это начало. Традиционно. Скорость меньше земной. Луна отстает. В полнолуние скорость выше земной. Луна обгоняет Землю. Знание ей дает Земля. Коль уж мы заговорили о разгоне и торможении, не посчитать ли нам ускорение Луны? Ускорение это вектор. У нас есть два источника силы - Солнце и Земля, две силы и две компоненты ускорения - к Солнцу и к Земле. Найдем их и оценим игру сил, кто там верховодит... Справимся?
Можно попробовать. Ускорение это ведь, кажется, производная от скорости? Только наверное лучше в другой ветке, а то тут уже ничего не видно.
И еще раз, пожалуйста, скажите, какие значения вы подставили в уравнение, я хочу у себя "в экселе" получить график и с ним поэкспериментировать.
да, точно так и у меня