Рис. 1

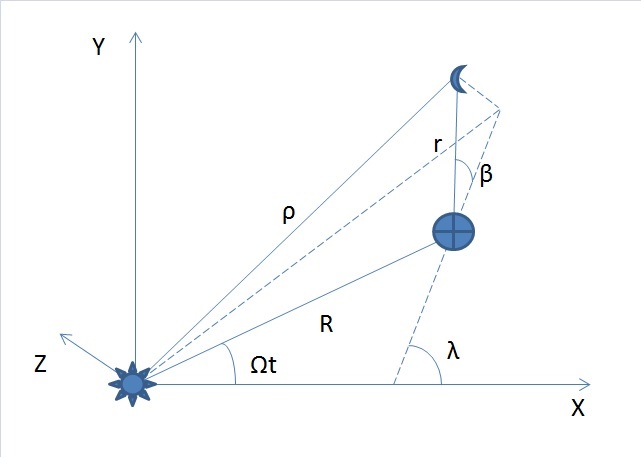
            Рассмотрим ограниченную круговую задачу трех тел в трехмерном пространстве (три степени свободы, три обобщенные координаты). Пусть Земля движется строго по окружности (Рис 1.) Выразим  гелиоцентрические координаты и соответствующие компоненты скорости Луны через углы ее прямого восхождения и склонения:

Уравнения движения можно получить, составив уравнения Лагранжа второго рода. Выражение для потенциальной энергии (отнесенной к массе Луны) очевидно и лаконично:

А вот для кинетической энергии Луны выражение весьма громоздко и поэтому не приводится.  Получение его  может стать неплохим упражнением  для желающих!

Взятие частных производных от кинетической энергии, выражение для которой содержит 7 слагаемых, я тоже опускаю.

Не тронув первое и второе, перейдем сразу к десерту.

Вот они, уравнения движения Луны:

Не вдаваясь в глубокий анализ этих уравнений, сразу решим их численно.

Начальные данные: перигей Луны 358000 км, скорость 1024 м/с, наклонение орбиты 5°.

Картина знакомая. Большая полуось «дышит» с периодом чуть менее 210 суток (Рис. 2).

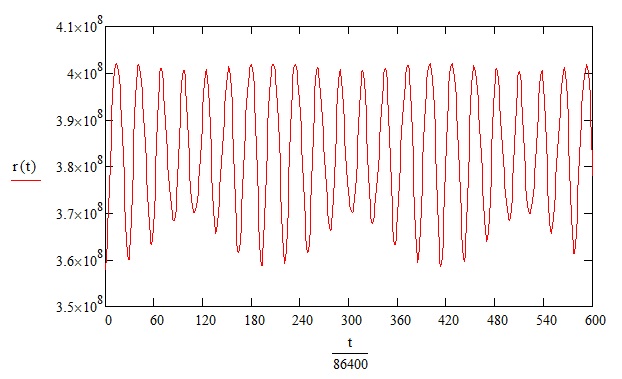
Рис. 2.

Фурье анализ прямого восхождения дает период обращения 27,32 суток (Рис. 3). Как доктор прописал!

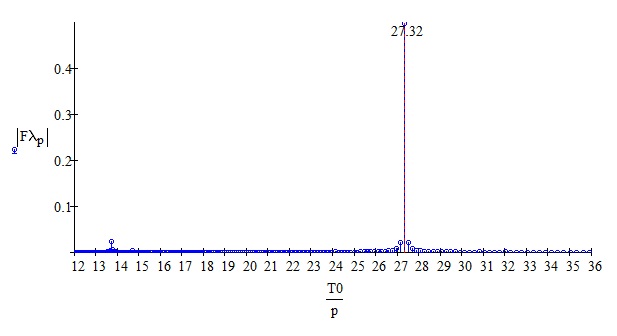
Рис. 3.

Но самое интересное в другом. Луна в своем вращении вокруг Земли это волчок, ось которого наклонена к оси орбитального движения Земли. Тут видимо не обойдется без прецессии…

Теперь, когда координаты и скорость Луны известны в любой момент времени (4), можно представить, как ведет себя вектор орбитального момента Луны (ось волчка). Для этого достаточно построить проекцию этого вектора на плоскость эклиптики, т.е. посчитать всего две его компоненты (массу Луны считаем равной единице):

 Расчетный отрезок времени – 9,3 года (Рис. 4). Конец вектора описал половину окружности! Модель неплохо отражает реальное положение дел, ведь мы знаем, что прецессионное движение лунного узла имеет период 18,6 лет.

 Какая же сила вызывает прецессию? Ответ прост: сила Кориолиса.

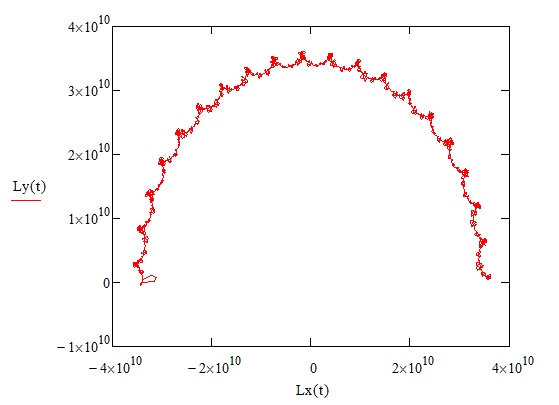
Рис. 4.

К сожалению, полный цикл адекватно рассчитать не удается из-за ограничений численного метода.

Тем не менее, вывод можно сделать такой: в движении Луны при всей его сложности нет ничего удивительного, все объяснимо в рамках теоретической механики и Лагранжева формализма!