Любой школьник знает, что период прецессии земной оси что-то около 26000 лет. Но как рассчитать данную величину? Здесь школьных знаний может не хватить. Известные мне работы достаточно сложны для понимания неспециалиста. Возьму на себя смелость утверждать, что мне удалось получить самый простой способ расчета периода лунно-солнечной прецессии.

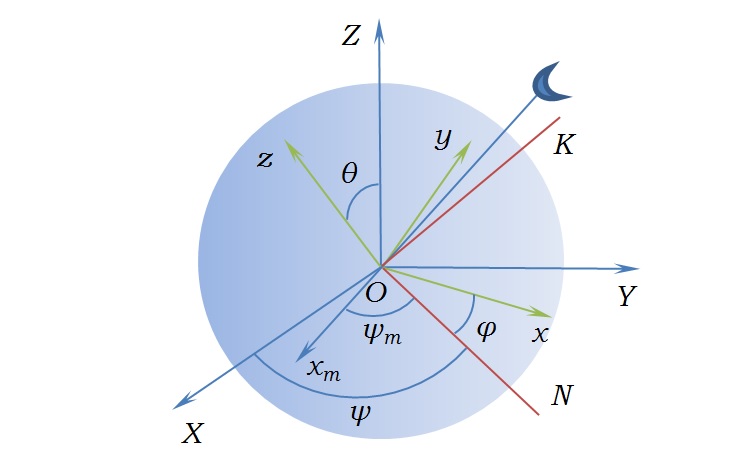
                Все дело в выборе системы координат. Это вращающаяся система координат (ONKz), угловая скорость которой $\Omega$ отличается от угловой скорости Земли $\omega$, т.е. базис этой системы подвижен как в инерциальном пространстве (OXYZ) так и относительно тела (Рис. 1). Выбор такой системы возможен только для осесимметричного тела ("экваториальные" осевые моменты инерции равны, A=B).  Допустим также, что вектор кинетического момента Земли пренебрежимо мало отклоняется от оси z. В результате мы получим «укороченные» уравнения движения [1]:

$\\\dot\psi=\frac{M_N}{C\omega\sin\theta} \\\dot\theta=-\frac{M_K}{C\omega}\\\dot\omega=\frac{M_z}{C}$    (1)

где $M_N, M_K, M_z$ - проекции гравитационного опрокидывающего момента от Луны, C- полярный момент инерции Земли.

                Нам известны проекции момента от Луны на оси собственной системы координат Oxyz, жестко связанной с Землей [2]:

$\\ {M_x}=\frac{3\mu}{R^3}(C-B)a_{12}a_{13}\\{M_y}=\frac{3\mu}{R^3}(A-C)a_{11}a_{13}\\{M_z}=\frac{3\mu}{R^3}(B-A)a_{11}a_{12}$                                (2)

где $\mu$ – гравитационный параметр Луны, R – расстояние от Земли до Луны, а направляющие косинусы выражаются через углы Эйлера:

$a_{11}=\cos\psi \cos\varphi - \sin\psi \cos\theta \sin\varphi\\a_{12}= - \cos\psi \sin\varphi - \sin\psi\cos\theta  \cos\varphi\\a_{13} =\sin\psi \sin\theta$                          (3)

                Нужно найти проекции этого момента на оси системы координат ONKz.Это очень просто сделать, поскольку система ONKz совмещается с системой Оxyz поворотом на угол $\varphi$ вокруг оси z.

Тогда

$\\M_N=M_x\cos\varphi-M_y\sin\varphi\\M_K=M_x\sin\varphi+M_y\cos\varphi\\M_z\: =\: \: 0$           (4)

                В произвольный момент времени угол прецессии Луны равен

$\psi_m =\psi-\Omega_m t$,                           (5)

где $\Omega_m$ – угловая скорость обращения Луны вокруг Земли. Будем считать расстояние от Земли до Луны постоянным.

                Аккуратно перемножив все синусы и косинусы, мы получим:

$\\M_N=-\frac{3\mu}{R^3}(C-A)\sin^2(\psi-\Omega_m t)\sin\theta\cos\theta\\M_K= -\frac{3\mu}{2R^3}(C-A)\sin2(\psi-\Omega_m t)\sin\theta\\M_z=0$                        (6)

                Теперь найдем среднее значение момента $M_N$ за один оборот Луны:

$\\\overline{M_N}=-\frac{3\mu}{2R^3}(C-A)\sin\theta\cos\theta$                       (7)
                Опрокидывающий момент от Солнца рассчитывается точно также. Соответственно суммарное действие Луны и Солнца в среднем создает момент на ось ON (линию узлов):

$\\\overline{M_N}_{ms}=-\frac{3}{2}\left(\frac{\lambda}{R^3_s}+\frac{\mu}{R^3_m}\right)(C-A)\sin\theta\cos\theta$                         (8)

Введем обозначение :

$H=\frac{C-A}{C}$                              (9)

Эта величина носит название «параметр прецессии» или «динамическое сжатие» Земли.

Теперь мы можем посчитать среднее значение угловой скорости прецессии Земли, вызванной двумя небесными телами – Солнцем и Луной:

$\\\overline{\dot\psi}_{ms}=-\frac{3}{2}\left(\frac{\lambda}{R^3_s}+\frac{\mu}{R^3_m}\right)\frac{H}{\omega}\cos\theta$                               (10)

Подставляя числовые значения, получим:

$\\\overline{\dot\psi}_{ms}=-7.804\cdot10^{-12}$, что соответствует периоду прецессии 25512 лет. Неплохо!

Система работает! Теперь можно оценить действие приливного момента. Но это уже другая история.

Литература.

1. Виттенбург Й. Динамика систем твердых тел. М.: Мир, 1980.
2. Белецкий В. В. Движение искусственного спутника Земли относительно центра масс. — М.: Наука, 1965.