Проекты № 16-42-732113 и № 16-42-732119 офим-м РФФИ (3)
III. Гидродинамические подстановки в задачах астрофизики
1. Метод гидродинамических подстановок
Общая идея гидродинамических подстановк былп изложена в работах [Zh10U,ZhZnIPVR12], и используется для решения задач гидродинамики пылевидной среды, а также для некоторых задач теории плазмы.
1.1. Общая схема метода гидродинамических подстановок
Задачи, которые будут рассматриваться в данном разделе отчета относятся к задачам гидродинамики, уравнения которых могут быть сведены к одномерным уравнениям Эйлера или Навье-Стокса. Сами течения в реальности могут иметь двумерное или трехмерное воплощение, но со специальным типом симметрии, например, цилиндрической или сферической.
Течения жидкости или газа, сводящиеся к одномерным уравнениям гидродинамики, целиком описываются с помощью задания поля скорости среды $u(x,t)$ как функции координаты и времени. Состояние среды при этом описывается ее плотностью $\rho$ и давлением $p(x,t)$. С каждой точкой среды можно формально связать маркерную функцию $\theta=\theta(x,t)$, значения которой привязаны к точкам среды. Это означает, что уравнение переноса маркеров, связанных с $\theta$, можно записать в следующем виде: $$\theta_t+u(x,t)\theta_x=0.\tag{1.1}\label{EqMark1}$$
Дифференциальным следствием этого соотношения является уравнение неразрывности: $$\frac{\partial}{\partial t}\rho+\frac{\partial}{\partial x}\Big(u\rho\Big)=0,\tag{1.2}\label{EqConM1}$$ с плотностью среды: $$\rho=\theta_x,\tag{1.3}\label{Defrho}$$ которое получается простым дифференцированием (\ref{EqMark1}) по $x$.
Это общее наблюдение позволяет рассмотреть специальный подход для конструирования моделей динамики среды, опирающийся на свойства функции маркера $\theta$. Суть метода состоит в том, чтобы используя свойства маркеров, найти подходящий вид поля скорости $v(x,t)$, как функции от $\theta$ и ее производных, такой, что объемные силы, действующие на среду, приобретают нужную форму. Именно тип действующих сил и определяет характер модели. Такой подход меняет общий взгляд на возможности анализа, нелинейных по своей сути, уравнений гидродинамики. Как подсказывает интуиция, попытка построить решение гидродинамической задачи с помощью какой-либо суперпозиции поля, заранее обречена на провал, поскольку уравнения гидродинамики нелинейны. Однако рассматриваемый подход демонстрирует существование особого типа суперпозиции в гидродинамике, а именно возможность разложить поле скорости на отдельные аддитивные составляющие, отвечающие за различающиеся по физической сущности объемные силы, которые, как правило, обладают свойством суперпозиции в соответствии с теорией тяготения Ньютона.
В качестве простого примера рассмотрим еще одно формальное тождество (кроме (\ref{EqConM1})), которое получается из уравнения переноса маркера. Дифференцируя уравнение неразрывности (\ref{EqConM1}), находим: $$\frac{\partial}{\partial t}\theta_x+u\frac{\partial}{\partial x}\theta_x=-u_x\theta_x,\tag{1.4}\label{Equxgtx}$$ или $$\frac{\partial}{\partial\theta}\ln \theta_x+u\frac{\partial}{\partial x}\ln \theta_x=-u_x.\tag{1.5}\label{Equx}$$ Важным является то, что эти тождества выглядят как результат действия оператора переноса: $${\hat L}=\frac{\partial}{\partial t}+v(x,t)\frac{\partial}{\partial x}\tag{1.6}\label{DefL}$$ на некоторые функции, связанные с маркером.
В качестве простого примера рассмотрим еще одно формальное тождество (кроме (\ref{EqConM1})), которое получается из уравнения переноса маркера. Дифференцируя уравнение неразрывности (\ref{EqConM1}), находим: $$\frac{\partial}{\partial t}\theta_x+u\frac{\partial}{\partial x}\theta_x=-u_x\theta_x,\tag{1.4}\label{Equxgtx}$$ или $$\frac{\partial}{\partial\theta}\ln \theta_x+u\frac{\partial}{\partial x}\ln \theta_x=-u_x.\tag{1.5}\label{Equx}$$ Важным является то, что эти тождества выглядят как результат действия оператора переноса: $${\hat L}=\frac{\partial}{\partial t}+v(x,t)\frac{\partial}{\partial x}\tag{1.6}\label{DefL}$$ на некоторые функции, связанные с маркером.
Продифференцируем теперь тождество (\ref{Equx}) еще раз по $x$. Следствием является следующее тождество: $${\hat L}\frac{\partial \ln \theta_x}{\partial x}=-u_{xx}-u_x\ln \theta_x=
-\frac{1}{\rho}\frac{\partial}{\partial x}(\rho u_x),\tag{1.7}\label{Equxx}$$ где $\rho=\theta_x$. Рассмотрим теперь в качестве поля скорости следующую функцию: $$u=U(\theta)-\nu \frac{\partial}{\partial x}\ln \theta_x.\tag{1.8}\label{Moduxx}$$
В этом случае уравнение для поля скорости с учетом имеющихся тождеств принимает вид уравнения Навье-Стокса для инерциального течения вязкого неоднородного газа с коэффициентом кинематической вязкости $\nu$ и динамической вязкости $\mu=\nu \rho$: $${\hat L} u= u_t+uu_x=\frac{1}{\rho}\frac{\partial}{\partial x}\Big(\nu\rho u_x\Big).\tag{1.9}\label{EqNSrho}$$ Решение этого уравнения строится на основе решений уравнения теплопроводности следующего вида: $$\theta_t+U(\theta)\theta_x=\nu\theta_{xx}.\tag{1.10}\label{EqgtT}$$
В этом уравнении $U(\theta)$ - произвольная дифференцируемая функция маркера. Начальное условие для $\theta$ и выбор функции $U(\theta)$ определяют решение начальной задачи с заданным начальным распределением и скорости, и плотности среды. Однако уравнение (\ref{EqgtT}) интегрируется полностью только в случае, если: $$U(\theta) = U_0+U_1\theta,\tag{1.11}\label{RedToBurg}$$ где $U_0$ и $U_1$ - произвольные вещественные постоянные. Выбор (\ref{RedToBurg}) сводит задачу в случае $U_1\not= 0$ к уравнению Бюргерса [Burgers], решение которого строится с помощью подстановки Коула-Хопфа: $$\theta = -2\nu \frac{\partial}{\partial x}\ln \phi,$$ как это было описано в [Hopf,Cole,Wizem]. Здесь $\phi(x,t)$ - вспомогательная функция, которая удовлетворяет уравнению теплопроводности: $$\phi_t+U_0\phi + U_1\phi_x=\nu\phi_{xx}.\tag{1.12}\label{EqTCF}$$ Решение системыы (\ref{EqNSrho}) и (1.2) для $u(x,t)$ и $\rho(x,t)$ можно записаить теперь в виде: $$u(x,t)=U_0-2U_1\nu \frac{\partial}{\partial x}\ln \phi-\nu \frac{\partial}{\partial x}\ln\left( \frac{\partial^2}{\partial x^2}\ln \phi\right),$$ $$\rho(x,t)=-2\nu \frac{\partial^2}{\partial x^2}\ln \phi.$$ Уравнение (\ref{EqNSrho}) по форме не очень сильно отличается от уравнения Бюргерса, но оно включено в более приемлемую, с точки зрения гидродинамики, систему, содержащую уравнение неразрывности (\ref{EqConM1}). Поэтому подстановка (1.8) в результате оказывается более сложной, чем подстановка Коула-Хопфа, сводящая уравнение Бюргерса к тому же уравнению теплопроводности.
В этом уравнении $U(\theta)$ - произвольная дифференцируемая функция маркера. Начальное условие для $\theta$ и выбор функции $U(\theta)$ определяют решение начальной задачи с заданным начальным распределением и скорости, и плотности среды. Однако уравнение (\ref{EqgtT}) интегрируется полностью только в случае, если: $$U(\theta) = U_0+U_1\theta,\tag{1.11}\label{RedToBurg}$$ где $U_0$ и $U_1$ - произвольные вещественные постоянные. Выбор (\ref{RedToBurg}) сводит задачу в случае $U_1\not= 0$ к уравнению Бюргерса [Burgers], решение которого строится с помощью подстановки Коула-Хопфа: $$\theta = -2\nu \frac{\partial}{\partial x}\ln \phi,$$ как это было описано в [Hopf,Cole,Wizem]. Здесь $\phi(x,t)$ - вспомогательная функция, которая удовлетворяет уравнению теплопроводности: $$\phi_t+U_0\phi + U_1\phi_x=\nu\phi_{xx}.\tag{1.12}\label{EqTCF}$$ Решение системыы (\ref{EqNSrho}) и (1.2) для $u(x,t)$ и $\rho(x,t)$ можно записаить теперь в виде: $$u(x,t)=U_0-2U_1\nu \frac{\partial}{\partial x}\ln \phi-\nu \frac{\partial}{\partial x}\ln\left( \frac{\partial^2}{\partial x^2}\ln \phi\right),$$ $$\rho(x,t)=-2\nu \frac{\partial^2}{\partial x^2}\ln \phi.$$ Уравнение (\ref{EqNSrho}) по форме не очень сильно отличается от уравнения Бюргерса, но оно включено в более приемлемую, с точки зрения гидродинамики, систему, содержащую уравнение неразрывности (\ref{EqConM1}). Поэтому подстановка (1.8) в результате оказывается более сложной, чем подстановка Коула-Хопфа, сводящая уравнение Бюргерса к тому же уравнению теплопроводности.
1.2. Адиабатические течения газа
Рассмотрим теперь задачу об адиабатическом течении идеальной сжимаемой среды. Как известно [Hydro], в одномерном случае система уравнений динамики таких течений описывается уравнениями: $$u_t+uu_x=-\frac{1}{\rho}p_x,\ \ \rho_t+\Big(\rho u\Big)_x=0,\ \ s_t+us_x=0,~~p=p(\rho,s),\tag{1.13}\label{EqAFG}$$ где $p=p(\rho,s)$ - давление, а $s$ - плотность энтропии течения. При адиабатическом течении энтропия элементарного объема жидкости переносимого течением сохраняется, что отражено в предпоследнем уравнении данной системы. В силу этого, энтропия $s$ должна быть связана с маркером $\theta$ общей функциональной зависимостью: $s=S(\theta)$. Отсюда следует, что давление $p$ можно записать как функцию вида: $p=p(\rho,\theta)$. В частном случае распределение энтропии среды может быть однородным $s=s_0={\rm const}$. В этом случае уравнение состояния выглядит наиболее просто: $p=p(\rho)$.
Для случая однородного распределения энтропии по пространству решение для поля скорости можно искать в следующей форме: $$u=W(\theta_x)=W(\rho),\tag{1.14}\label{DefuP}$$ где $W(\rho)$ - некоторая дифференцируемая функция своего аргумента. Применяя к такому полю скорости оператор переноса ${\hat L}$ и учитывая (\ref{Equxgtx}), приходим к следующему общему соотношению:$${\hat L}u =u_t+uu_x = -u_x W'(\theta_x)\theta_x = -\rho_x [W'(\rho)]^2\rho=-\frac{1}{\rho}\frac{\partial}{\partial x}P(\rho),$$ где, как и раньше, $\rho=\theta_x$ и $$P(\rho) = \int [W'(\rho)]^2\rho^2d \rho.\tag{1.15}\label{DefPW}$$
В частности, в случае идеального газа: $p=K\rho^{\gamma}$, где $\gamma$ - показатель адиабаты. Отсюда может быть вычислена функция $W(\rho)$. Имеем: $$W'(\rho) = \sqrt{K \frac{\gamma}{\gamma-2}} \rho^{\gamma/2-1}$$ и окончательно: $$W= \sqrt{\frac{4K}{\gamma(\gamma-2)}}\rho^{\gamma/2}+W_0.\tag{1.16}\label{SolW}$$ Для маркера уравнение примет такой вид: $$\theta_t+ W(\rho)\theta_x=0.\tag{1.17}\label{EqMarkW}$$ После дифференцирования по $x$ это уравнение принимает вид уравнения Хопфа: $$\rho_t+ \Big(\alpha \rho^{\gamma/2}+W_0\Big)\rho_x=0,~~\alpha= \Big(\frac{\gamma}{2}+1\Big)\sqrt{\frac{4K}{\gamma(\gamma-2)}}.\tag{1.18}\label{EqHW}$$ Решение этого уравнения вычисляется из решения алгебраического (или трансцендентного) уравнения: $$\rho=H\Big(x-(\alpha \rho^{\gamma/2}+W_0) t\Big),\tag{1.19}\label{SolrhoBT}$$ где $H(\xi)$ - функция, задаваемая начальным распределением плотности: $$\rho(x,0)=H(x).$$ Это известное решение имеет тот недостаток, что существует только для таких типов начальных распределений поля скорости и плотности, которые заранее связаны соотношением (\ref{DefuP}). Решение общей задачи будет рассмотрено далее, но предварительно приведем решения нескольких других задач течения сжимаемой среды.
1.3. Течения самогравитирующей пыли. Общая формулировка задачи
Развитый метод можно использовать для решения более широкого круга задач, в частности, для решения задач динамики самогравитирующей пыли. Метод был предложен в работах [Zh10U,ZhZnIPVR12]. В этом случае к уравнениям гидродинамики необходимо добавить уравнение Пуассона для потенциала поля тяготения, созданного самой пылью. Самосогласованная система уравнений имеет следующий вид: $$u_t+uu_x=-\phi_x,~~~\rho_t+\frac{1}{x^n}\frac{\partial}{\partial x}\Big(x^{n}u\rho\Big)=0,\tag{1.20}\label{EqSG}$$ $$\frac{1}{x^n}\frac{\partial}{\partial x}\Big(x^n\phi_x\Big)=4\pi G\rho.\tag{1.21}\label{EqPoisson}$$ Уравнения (\ref{EqSG}) - уравнения Эйлера, уравнение (\ref{EqPoisson}) - уравнение Пуассона. Уравнение состояния пыли эквивалентно требованию равенства давления нулю, поэтому силы Архимеда в данной системе нет. Здесь $\phi(x,t)$ - потенциал гравитационного поля, $G$ - постоянная тяготения Ньютона, а целое число $n=0,1,2$ - соответствует координатной размерности задачи $d=n+1$. В случае $n=0$ - это задача с плоской симметрией, $n=1$ - задача с цилиндрической симметрией, а в случае с $n=2$ - сферической.
Физическая постановка задач, связанных с системой (\ref{EqSG})-(\ref{EqPoisson}), состоит в описании процесса формирования плотных компактных объектов из рассеянных скоплений пыли под действием собственного поля тяготения. Поскольку процесс формирования плотных объектов из пыли происходит без силы Архимеда, то он практически всегда [GZ95UFN] заканчивается образованием сингулярности в распределении плотности. Одним из важных параметров этого процесса является время образования сингулярности из начального состояния. Также возможно образование различного типа волн, в том числе ударных, в процессе формирования плотного объекта, которые могут возникать при не нулевых начальных распределениях поля скорости. Для решения этих задач мы и воспользуемся методом гидродинамических подстановок.
2. Течения самогравитирующей пыли
2.1. Течния с плоской симметрией
Построение решения начнем со случая $n=0$. Подставляя (\ref{Defrho}) в (\ref{EqPoisson}) и затем интегрируя по $x$, получаем уравнение следующего вида: $$\phi_x = g_0(t)+ 4\pi G \theta.\tag{2.1}\label{DefMarkG}$$ Здесь $g_0(t)$ - постоянная интегрирования по х, характеризующая фактически ускорение системы отсчета. Теперь подставляя это соотношение в первое уравнение (\ref{EqSG}), преобразуем его к следующему виду: $$u_t+uu_x = -4\pi G \theta - g_0(t).\tag{2.2}\label{EqEulerG}$$
Суть этого соотношения состоит в том, что гидродинамическим маркером одномерного самогравитирующего течения пыли является ускорение свободного падения $g=\phi_x$ (при $g_0(t)=0$). Это означает, что все точки пыли сохраняют при своем движении ту величину ускорения свободного падения, которая существовала в начальный момент времени. Этот результат, кажущийся достаточно случайным, является, на самом деле, общим свойством самогравитирующих структур без давления. Обобщение этого вывода мы рассмотрим далее.
Решение для поля скорости будем искать в следующем общем виде: $$u(x,t)= U(\theta)+ h(t)\theta + v_0(t).\tag{2.3}\label{SubsuG0}$$ Действуя на эту функцию оператором переноса ${\hat L}$, находим: $${\hat L}u= \theta\dot{h} + \dot{v}_0(t).$$ Сравнивая это соотношение с (\ref{EqEulerG}), получаем: $$h(t) = -4\pi G t +h_0,\ \ \dot{v}_0=-g_0(t).\tag{2.4}\label{Eqh}$$
Таким образом, решения исходной системы уравнений строятся, исходя из решений уравнения для маркера: $$\theta_t + \Big(U(\theta)+(-4\pi G t +h_0)\theta+v_0(t)\Big)\theta_x=0.\tag{2.5}\label{EqMarkSG0}$$ Это уравнение имеет неявное решение: $$\theta=H\Big(x-U(\theta)t+(2\pi G t^2 - h_0 t)\theta-x_0(t)\Big).\tag{2.6}\label{SolgtSG0}$$ Здесь $H(\xi)$ - произвольная дифференцируемая функция аргумента: $$\xi=x-U(\theta)t+(2\pi G t^2 - h_0 t)\theta-x_0(t),\ \ \ x_0(t)=\int v_0(t)dt.$$ Функция $H(\xi)$ определяется начальным распределением маркера в пространстве: $$\theta(x,0)=H\Big(x-x_0(0)\Big),$$ которое связано с начальным распределением массы: $$\rho(x,0)=\left.\theta_x\right|_{t=0}=H'\Big(x-x_0(0)\Big).$$ Начальное распределение скорости задается функцией $U(\theta)$: $$u(x,0)=U\Big(\theta(x,0)\Big)+ h_0 \theta(x,0)+v_0(0).$$
Заметим, что масса среды, сосредоточенная в интервале координат $[x_1,x_2]$, определяется разностью значений маркера: $$M_{[x_1,x_2]}(t)=\int\limits_{x_1}^{x_2}\theta_x dx =\theta(x_2,t)-\theta(x_1,t)\tag{2.7}\label{DefMass0}$$ Важной характеристикой распределения масс является полная масса среды: $$M_0=\theta(\infty,t)-\theta(-\infty,t).$$ Для астрофизических приложений необходимо рассматривать такие распределения массы в пространстве, для которых полная масса пыли должна оставаться конечной и постоянной во времени в случае бесконечного интервала $[x_1,x_2]$. Последнее условие означает, что нет самопроизвольного притока или оттока массы в систему, что обеспечивается в силу выполнения уравнения неразрывности нулевыми значениями скорости потока на бесконечности: $u(\infty,t)=u(-\infty,t)=0$. Отсутствие среднего перемещения центра масс всей системы в пространстве должно соответствовать условию: $$V_0 = \frac{d}{dt}\int\limits_{-\infty}^{\infty}x \rho dx= \int\limits_{-\infty}^{\infty} x\rho_t dx=-\int\limits_{-\infty}^{\infty} x\frac{\partial}{\partial x}(u\rho) dx=\int\limits_{-\infty}^{\infty}u(x,t)\rho dx=0.\tag{2.8}\label{DefV0}$$
Решение для $\theta$ (\ref{SolgtSG0}) допускает возникновение сингулярностей в распределении массы за конечное время. Момент образования сингулярности определяется, как и в случае определения момента опрокидывания простой волны, первым моментом появления точки $(x_*,t_*)$, в которой плотность обращается в бесконечность: $\rho(x_*,t_*)=\infty$. Этот момент определяется с помощью вычисления производной $\theta_x$ из общего решения (\ref{SolgtSG0}). Имеем: $$\theta_x = H'(\xi)\Big(1-U'(\theta)\theta_x+(2\pi G t^2 - h_0 t)\theta_x\Big),$$ Отсюда находим: $$\rho=\theta_x= \frac{H'(\xi)}{1+H'(\xi)[U'(\theta)-(2\pi G t^2 - h_0 t)]}.\tag{2.9}\label{SolrhoSG}$$ Первый момент образования сингулярности определяется из условия обращения знаменателя этого соотношения в ноль. Для иллюстрации выводов общего анализа приведем несколько примеров (частично приведенных в [ZhZnIPVR12,Zh17STFI]).
Наиболее простой случай соответствует классической задаче Джинса, когда начальные распределения плотности и скорости однородны: $\rho(x,0)=\rho_0={\rm const},\ \ u(x,0)=0$. Выбор однородного значения скорости, равного нулю, лишь фиксирует выбор определенной системы отсчета. Однородное же распределение массы соответствует бесконечной суммарной массе на бесконечном пространственном интервале. При таких начальных условиях имеем:
$$U(\theta)\equiv 0,\ \ \theta(x,0)=\alpha x + \theta_0,\ \ H(\xi)=\alpha\xi+\theta_0+x_0(0),$$ где $\alpha$ и $\theta_0$ - вещественные постоянные. В этом случае решение имеет следующий вид: $$\theta = \alpha\Big(x+(2\pi G t^2 - h_0 t)\theta-x_0(t)\Big)+\theta_0+x_0(0).$$ Отсюда находим: $$\theta=\frac{\alpha (x - x_0(t))+x_0(0)+\theta_0}{1-2\pi G t^2 + h_0 t}.$$ Это решение демонстрирует конечный результат эволюции однородного распределения плотности. Оставаясь со временем однородным распределением, плотность за конечное время $t_*=1/\sqrt{2\pi G}$ в каждой точке пространства одновременно обращается в бесконечность. Этот результат можно рассматривать как вариант парадокса Неймана-Зелигера [Nov83] для плоско-симметричного распределения материи.
Более физически значимый пример можно получить, рассматривая следующее начальное распределение плотности типа распределения Лоренца: $$\rho(x,0) = \frac{\rho_0}{1+x^2/a^2},\tag{2.10}\label{Defrho0}$$ где $a={\rm const}$ - параметр, характеризующий ширину начального распределения Лоренца. Масса такого распределения конечна: $$M_0 = \rho_0\int\limits_{-\infty}^{\infty}\frac{dx}{1+x^2/a^2}=\pi \rho_0 a.$$ Функция $H(\xi)$ при таком начальном распределении имеет такой вид: $$\theta(x,0)=H(x-x_0(0))=\int\limits_{0}^x \rho(y,0) dy= \rho_0 a\ {\rm arctg}(x/a).$$ Начальное распределение скорости выберем, как и в простейшем случае, однородным с нулевым значением во всем пространстве. В силу этого $U(\theta)=0$. Решение для $\gt$ теперь находится из решения уравнения: $$\theta = \rho_0 a\ {\rm arctg}\Big(x/a+2\pi G t^2\theta/a\Big).$$ Здесь полагалось $x_0(t)=0$ и $h_0=0$. После отыскания решения для $\theta$, решения для $\rho(x,t)$ и $u(x,t)$ вычисляются с помощью соотношений: $$\rho(x,t)=\frac{\rho_0}{1+\Big(x+2\pi G t^2\theta\Big)/a^2-\rho_0 2\pi G t^2},$$ $$u(x,t) = - t \theta(x,t)=- t \rho_0 a\cdot {\rm arctg}\Big(x/a+2\pi G t^2\theta/a\Big).$$
Графики эволюции плотности и скорости для случая нулевого начального распределения скорости: $u(x,0)=0$, приведены на рисунках.
Таким образом, решения исходной системы уравнений строятся, исходя из решений уравнения для маркера: $$\theta_t + \Big(U(\theta)+(-4\pi G t +h_0)\theta+v_0(t)\Big)\theta_x=0.\tag{2.5}\label{EqMarkSG0}$$ Это уравнение имеет неявное решение: $$\theta=H\Big(x-U(\theta)t+(2\pi G t^2 - h_0 t)\theta-x_0(t)\Big).\tag{2.6}\label{SolgtSG0}$$ Здесь $H(\xi)$ - произвольная дифференцируемая функция аргумента: $$\xi=x-U(\theta)t+(2\pi G t^2 - h_0 t)\theta-x_0(t),\ \ \ x_0(t)=\int v_0(t)dt.$$ Функция $H(\xi)$ определяется начальным распределением маркера в пространстве: $$\theta(x,0)=H\Big(x-x_0(0)\Big),$$ которое связано с начальным распределением массы: $$\rho(x,0)=\left.\theta_x\right|_{t=0}=H'\Big(x-x_0(0)\Big).$$ Начальное распределение скорости задается функцией $U(\theta)$: $$u(x,0)=U\Big(\theta(x,0)\Big)+ h_0 \theta(x,0)+v_0(0).$$
Заметим, что масса среды, сосредоточенная в интервале координат $[x_1,x_2]$, определяется разностью значений маркера: $$M_{[x_1,x_2]}(t)=\int\limits_{x_1}^{x_2}\theta_x dx =\theta(x_2,t)-\theta(x_1,t)\tag{2.7}\label{DefMass0}$$ Важной характеристикой распределения масс является полная масса среды: $$M_0=\theta(\infty,t)-\theta(-\infty,t).$$ Для астрофизических приложений необходимо рассматривать такие распределения массы в пространстве, для которых полная масса пыли должна оставаться конечной и постоянной во времени в случае бесконечного интервала $[x_1,x_2]$. Последнее условие означает, что нет самопроизвольного притока или оттока массы в систему, что обеспечивается в силу выполнения уравнения неразрывности нулевыми значениями скорости потока на бесконечности: $u(\infty,t)=u(-\infty,t)=0$. Отсутствие среднего перемещения центра масс всей системы в пространстве должно соответствовать условию: $$V_0 = \frac{d}{dt}\int\limits_{-\infty}^{\infty}x \rho dx= \int\limits_{-\infty}^{\infty} x\rho_t dx=-\int\limits_{-\infty}^{\infty} x\frac{\partial}{\partial x}(u\rho) dx=\int\limits_{-\infty}^{\infty}u(x,t)\rho dx=0.\tag{2.8}\label{DefV0}$$
Решение для $\theta$ (\ref{SolgtSG0}) допускает возникновение сингулярностей в распределении массы за конечное время. Момент образования сингулярности определяется, как и в случае определения момента опрокидывания простой волны, первым моментом появления точки $(x_*,t_*)$, в которой плотность обращается в бесконечность: $\rho(x_*,t_*)=\infty$. Этот момент определяется с помощью вычисления производной $\theta_x$ из общего решения (\ref{SolgtSG0}). Имеем: $$\theta_x = H'(\xi)\Big(1-U'(\theta)\theta_x+(2\pi G t^2 - h_0 t)\theta_x\Big),$$ Отсюда находим: $$\rho=\theta_x= \frac{H'(\xi)}{1+H'(\xi)[U'(\theta)-(2\pi G t^2 - h_0 t)]}.\tag{2.9}\label{SolrhoSG}$$ Первый момент образования сингулярности определяется из условия обращения знаменателя этого соотношения в ноль. Для иллюстрации выводов общего анализа приведем несколько примеров (частично приведенных в [ZhZnIPVR12,Zh17STFI]).
Наиболее простой случай соответствует классической задаче Джинса, когда начальные распределения плотности и скорости однородны: $\rho(x,0)=\rho_0={\rm const},\ \ u(x,0)=0$. Выбор однородного значения скорости, равного нулю, лишь фиксирует выбор определенной системы отсчета. Однородное же распределение массы соответствует бесконечной суммарной массе на бесконечном пространственном интервале. При таких начальных условиях имеем:
$$U(\theta)\equiv 0,\ \ \theta(x,0)=\alpha x + \theta_0,\ \ H(\xi)=\alpha\xi+\theta_0+x_0(0),$$ где $\alpha$ и $\theta_0$ - вещественные постоянные. В этом случае решение имеет следующий вид: $$\theta = \alpha\Big(x+(2\pi G t^2 - h_0 t)\theta-x_0(t)\Big)+\theta_0+x_0(0).$$ Отсюда находим: $$\theta=\frac{\alpha (x - x_0(t))+x_0(0)+\theta_0}{1-2\pi G t^2 + h_0 t}.$$ Это решение демонстрирует конечный результат эволюции однородного распределения плотности. Оставаясь со временем однородным распределением, плотность за конечное время $t_*=1/\sqrt{2\pi G}$ в каждой точке пространства одновременно обращается в бесконечность. Этот результат можно рассматривать как вариант парадокса Неймана-Зелигера [Nov83] для плоско-симметричного распределения материи.
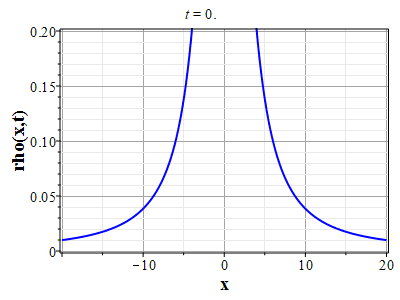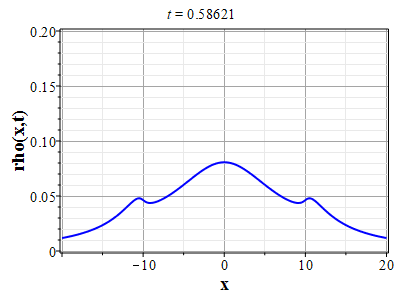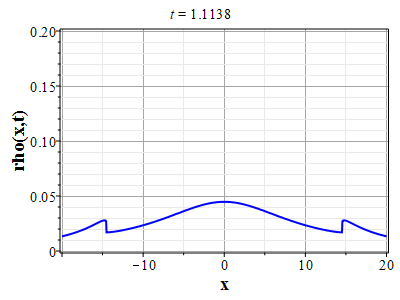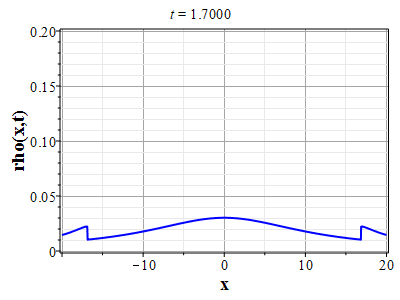
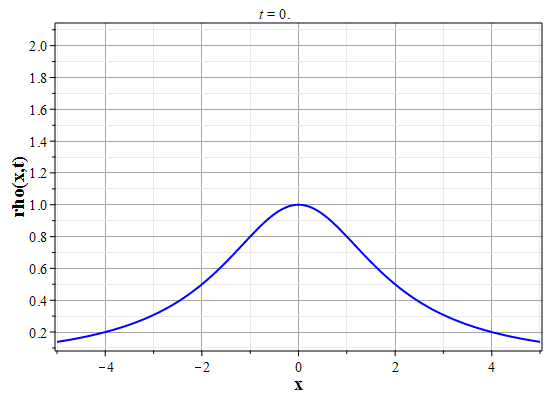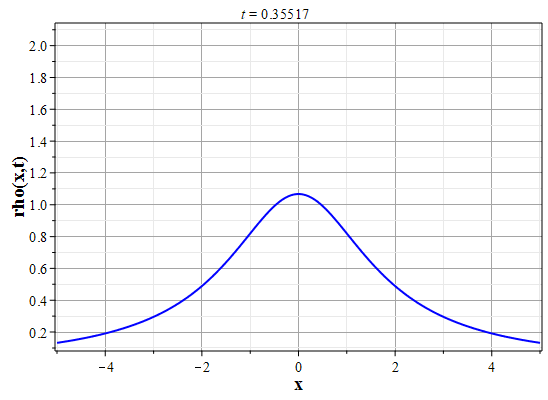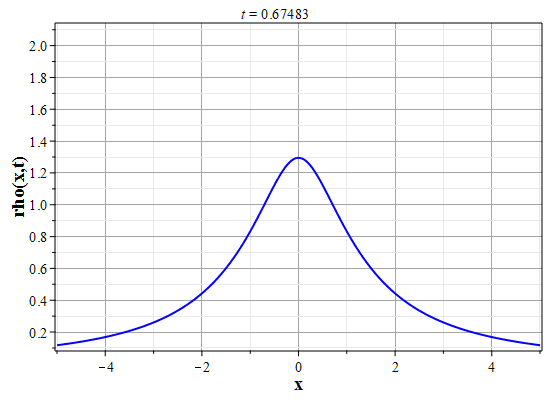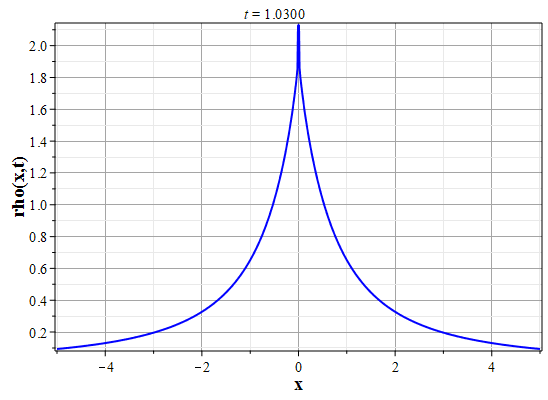
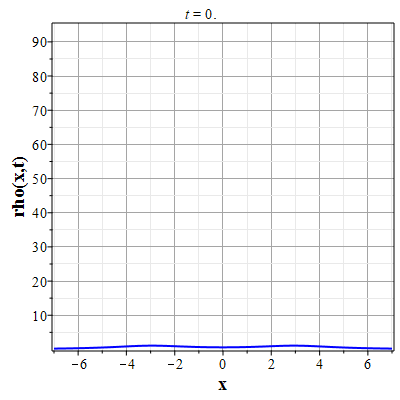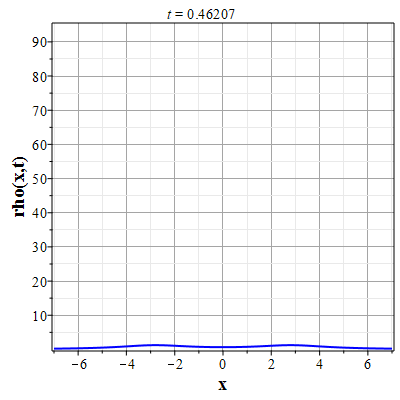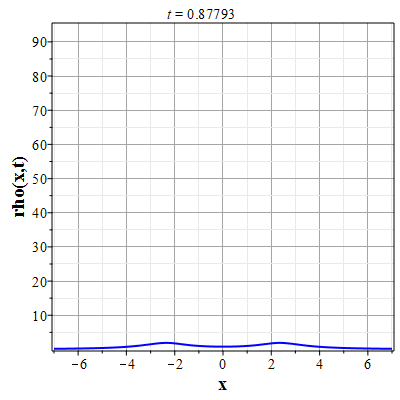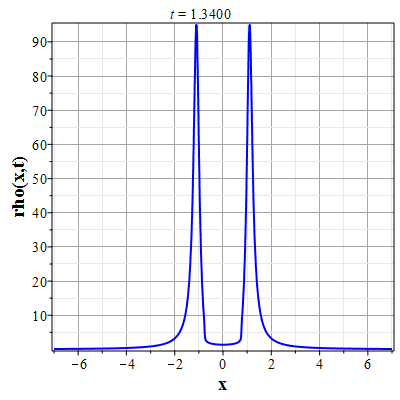
Более физически значимый пример можно получить, рассматривая следующее начальное распределение плотности типа распределения Лоренца: $$\rho(x,0) = \frac{\rho_0}{1+x^2/a^2},\tag{2.10}\label{Defrho0}$$ где $a={\rm const}$ - параметр, характеризующий ширину начального распределения Лоренца. Масса такого распределения конечна: $$M_0 = \rho_0\int\limits_{-\infty}^{\infty}\frac{dx}{1+x^2/a^2}=\pi \rho_0 a.$$ Функция $H(\xi)$ при таком начальном распределении имеет такой вид: $$\theta(x,0)=H(x-x_0(0))=\int\limits_{0}^x \rho(y,0) dy= \rho_0 a\ {\rm arctg}(x/a).$$ Начальное распределение скорости выберем, как и в простейшем случае, однородным с нулевым значением во всем пространстве. В силу этого $U(\theta)=0$. Решение для $\gt$ теперь находится из решения уравнения: $$\theta = \rho_0 a\ {\rm arctg}\Big(x/a+2\pi G t^2\theta/a\Big).$$ Здесь полагалось $x_0(t)=0$ и $h_0=0$. После отыскания решения для $\theta$, решения для $\rho(x,t)$ и $u(x,t)$ вычисляются с помощью соотношений: $$\rho(x,t)=\frac{\rho_0}{1+\Big(x+2\pi G t^2\theta\Big)/a^2-\rho_0 2\pi G t^2},$$ $$u(x,t) = - t \theta(x,t)=- t \rho_0 a\cdot {\rm arctg}\Big(x/a+2\pi G t^2\theta/a\Big).$$
Графики эволюции плотности и скорости для случая нулевого начального распределения скорости: $u(x,0)=0$, приведены на рисунках.
|
|
|
|
|
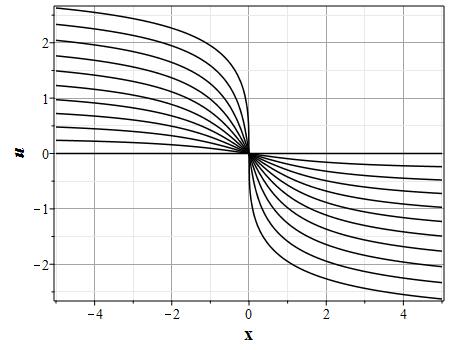
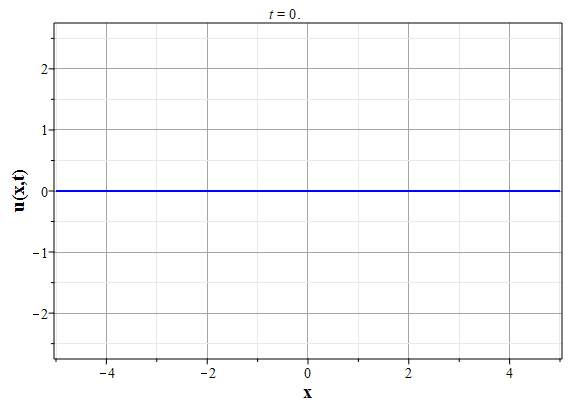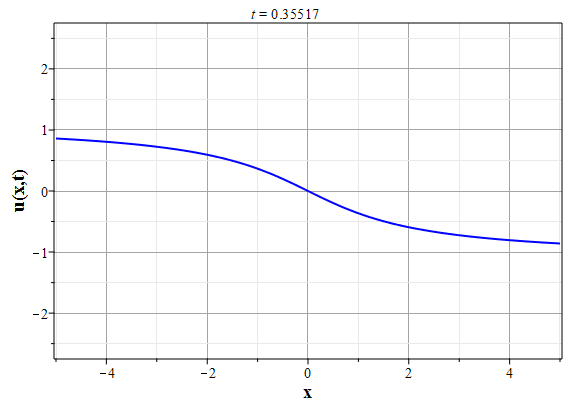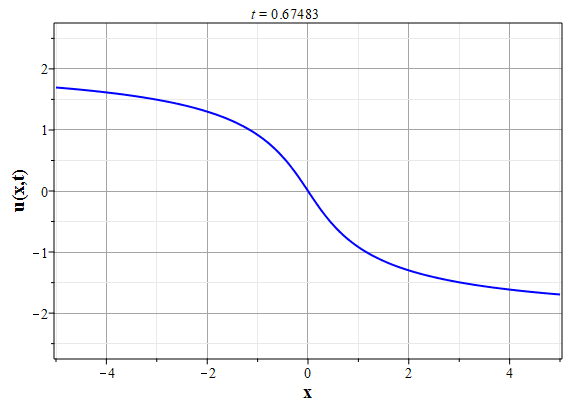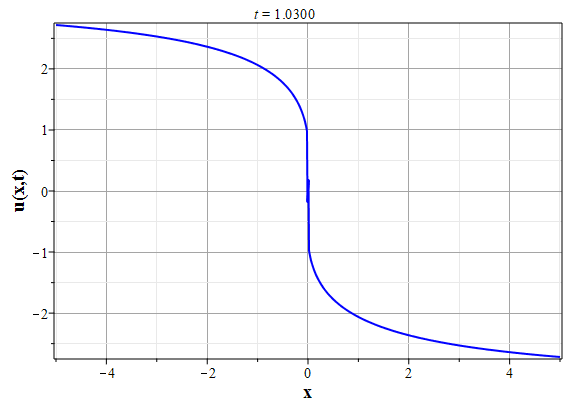 Рис. 4. Эволюция скорости потока для начального распределения плотности (2.10) и всюду нулевой начальной скорости потока до момента образования сингулярности (анимация) |
Из графиков и анимаций видно, что скорость увеличивается со временем во всем пространстве. На больших расстояних от первичной флуктуации скорость потока почти пространственно однородно. Это, очвидно, связано с тем, что плотность среды мала на больших расстояниях, а величина ускорения переносится как маркер. Поэтому среда во всем пространстве "ощущает" возникновение флуктуации.
Еще один пример построения решения для системы с плоской симметрией для $u(x,0)=0$ приведены на рис. \rf{Pic2}(a,b). Этот пример соответствует начальному распределению плотности в виде двух локальных флуктуаций: $$\rho(x,0) = \frac{\rho_0}{1+(x-b)^2/a^2}+\frac{\rho_0}{1+(x+b)^2/a^2},\ \ u(x,0)=0.\tag{2.11}\label{Defrho2}$$ для следующих значений параметров: $a=1,~b=3,\rho_0\pi = 1$. Соответствующее выражение для начального распределения маркера имеет следующий вид: $$\theta(x,0)=H(x-x_0(0))= \rho_0 a \Big({\rm arctg}((x-b)/a)+{\rm arctg}((x+b)/a)\Big).$$ Графики демонстрируют сближение на изображенном начальном отрезке времени двух флуктуаций за счет их гравитационного притяжения. При этом в максимуме каждой из флуктуаций формируются сингулярности (в конце изображенного отрезка времени), возникающие до момента их слияния.
|
Рис. 5. Эволюция плотности для |
Рис. 6. Эволюция скорости потока для |
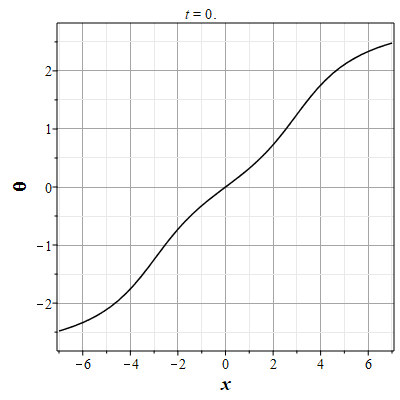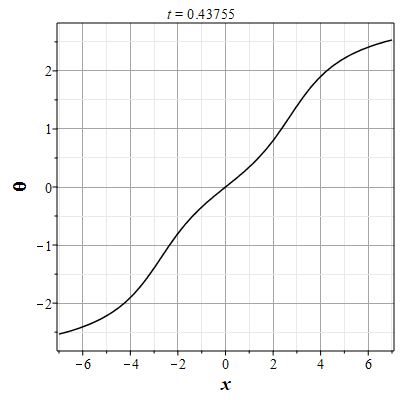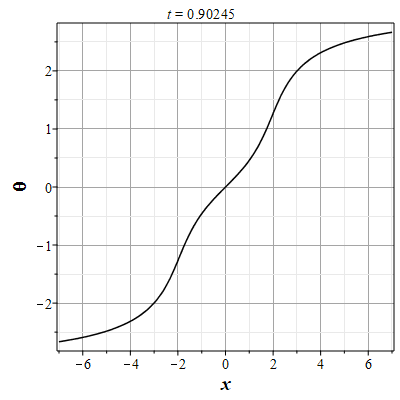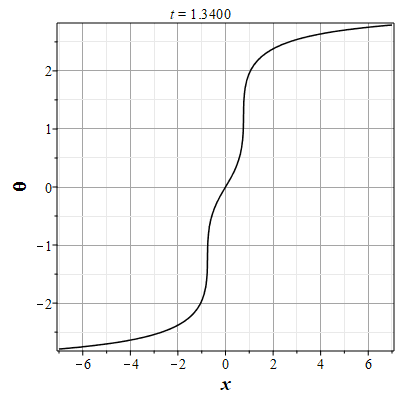 Рис. 7. Анимация эволюции маркера для начального распределения (2.11) и всюду нулевой скосрости потока |
|
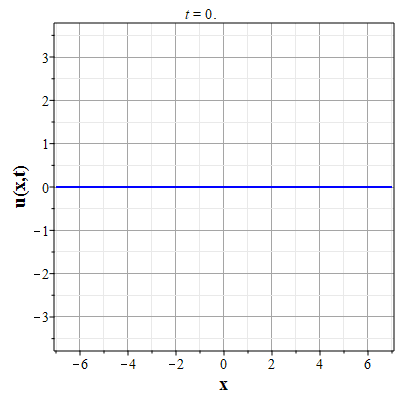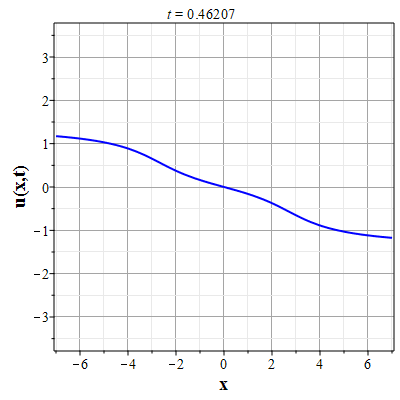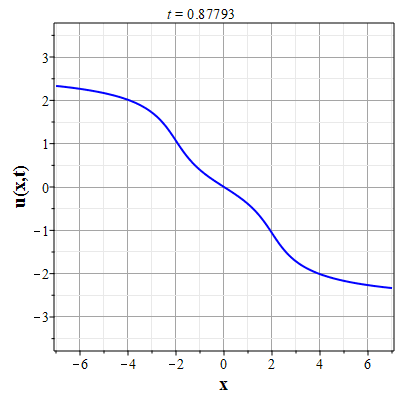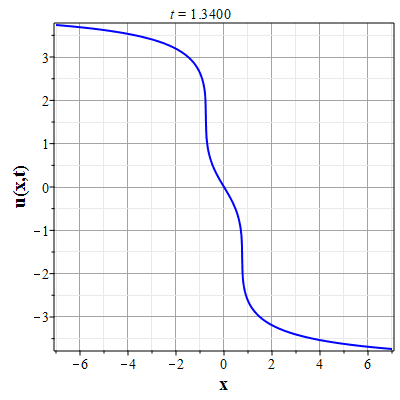 Рис. 9. Анимация эволюции скорости потока для начального распределения (2.11) и всюду нулевой скосрости потока |
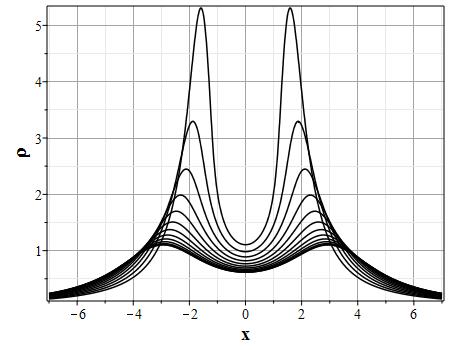
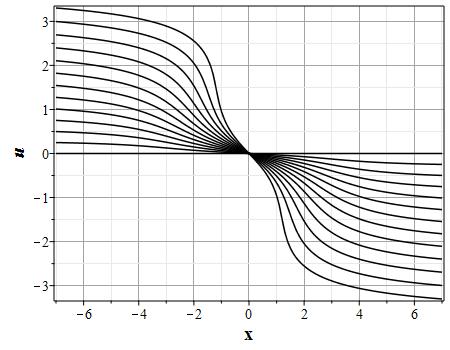
Вариант эволюции системы для начального распределения скорости: $$u(x,0)=-8\theta_0(x)(\theta^2_0(x)-\pi^2/4)\tag{2.12}\label{DefUbeg}$$ и начального распределения плотности \rf{Defrho0} приведен на рис. (10)-(15). Такой выбор начального распределения скорости соответствует выбору функции $U(\theta)=-\theta(\theta^2-\pi^2/4)$. На рис. (10)-(13) приведены графики эволюции распределения плотности, а на (14)-(15) скорости для указанных начальных распределений скорости и плотности. Рисунки (11) и (13) представляют увеличенное изображении графиков на (10) и (12) для более детального представления о формировании ударной волны плотности. В начальный момент времени вблизи начала координат, где находится максимум плотности, имеются максимумы поля скорости с направлением от начала координат. На изображенном начальном отрезке времени масса уносится потоком от максимума плотности, так что значение плотности в начале координат убывает. При этом на некотором расстоянии от начала координат формируются две ударных волны. При дальнейшей эволюции (за пределами изображенного отрезка времени) ударные волны останавливаются, а затем начинают двигаться симметрично к началу координат, так что через конечный отрезок времени в центре формируется единственная сингулярность.
|
|
.jpg) Рис. 11. Эволюции плотности (с большимразрешением по вертикали) для начального распределения плотности (2.11) и начального распределения скорости потка (2.12) |
.jpg)
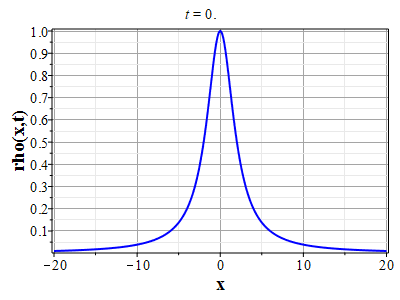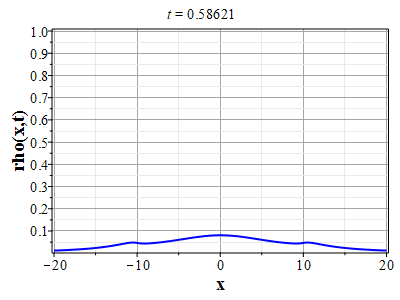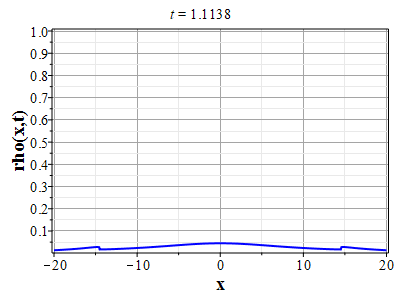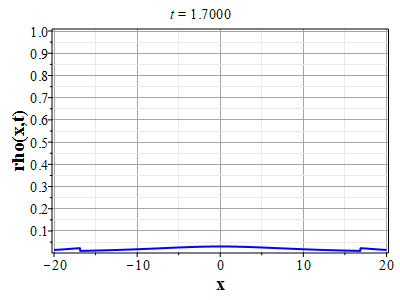 Рис. 12. Анимация эволюции плотности (сменьшим разрешением по вертикали) для начального распределения плотности (2.11) и начального распределения скорости потка (2.12) |
|
.jpg) Рис. 14. Эволюции скорости потока дляначального распределения плотности (2.11) и начального распределения скорости потка (2.12) |
 Рис. 15. Анимация эволюции скорости потока дляначального распределения плотности (2.11) и начального распределения скорости потка (2.12) |
2.2. Подстановка для течений с цилиндрической и сферической симметриями
Для реализации развитого подхода к интегрированию системы (\ref{EqSG}) в случае цилиндрической $n=1$ и сферической симметрий $n=2$ необходимо ввести замену переменных и несколько преобразовать уравнения. Одновременно получим и другое решение задачи с плоским фронтом на полупрямой. Вместо плотности введем новую функцию $R=x^n \rho$. В этом случае уравнения с функцией $R$ будут иметь такой вид: $$u_t+uu_x=-\phi_x,~~~R_t+\frac{\partial}{\partial x}\Big(R u\Big)=0,$$ $$\frac{\partial}{\partial x}\Big(x^n\phi_x\Big)=4\pi G R.$$ Для системы такого вида связь маркера $\theta$ с плотностью будет определяться следующим соотношением: $$ R =\theta_x=x^n\rho.$$ При этом уравнение неразрывности выполняется автоматически как и в одномерном случае. Интегрируя уравнение Пуассона, находим: $$\phi_x = \frac{1}{x^n}\Big(4\pi G \theta + g_0(t)\Big).\tag{2.13}\label{DefMarkGn}$$ Подставляя это выражение в уравнение для радиальной скорости $u(x,t)$, приводим его к следующему виду: $$u_t+uu_x= -\frac{1}{x^n}\Big(4\pi G \theta + g_0(t)\Big).\tag{2.14}\label{Equn}$$ Для простоты будем полагать, что $g_0(t)=g_0={\rm const}$.
Соотношение (\ref{DefMarkGn}) представляет собой обобщение соотношения (\ref{DefMarkG}) и показывает, что в случае цилиндрической и сферической симметрий маркером является ускорение свободного падения, умноженное на якобиан преобразования от декартовых координат, соответственно, к цилиндрическим ($n=1$) и сферическим ($n=2$). Это указывает на то, что данный факт не является случайным и отражает общее свойство гравитационного поля.
Гидродинамическую подстановку для $u$ будем искать в следующем виде: $$u= f(x)F(\theta).\tag{2.15}\label{DefSubsun}$$ Действуя на это соотношение оператором ${\hat L}$, получаем: $${\hat L}u = u f'(x)F(\theta)=f(x)f'(x)F^2(\theta)=-\frac{4\pi G}{x^n}(4\pi G \theta +g_0).\tag{2.16}\label{DefSubsu3}$$ Сравнивая правую часть этого выражения с (\ref{Equn}), находим условия, при которых они будут совпадать. Из условия разделения переменных находим: $$f(x)f'(x)=-\frac{\lambda^2}{x^n}.\tag{2.17}\label{Eqff}$$ В этом случае для функции $F(\theta)$ должно выполняться алгебраическое уравнение: $$F^2 = (4\pi G \theta+ g_0)/\lambda^2.\tag{2.18}\label{EqFgt}$$
Для функции $f(x)$ получаем следующие решения:$$f_n(x)=\left\{\begin{eqnarray*}&&\lambda\sqrt{2}\sqrt{a-x},\quad n=0\\&&\lambda\sqrt{2}\sqrt{\ln(a/x)}, \quad n=1\\&&\lambda\sqrt{2}\sqrt{a^{-1}+x^{-1}},\quad n=2\end{eqnarray*}\right.\tag{2.19}\label{Solf}$$ Здесь $a$ - постоянная интегрирования.
Соответственно, вычисляем решение для функции $F(\theta)$: $$F(\theta)=\sqrt{4\pi G \theta+g_0}/\lambda.\tag{2.20}\label{SolFgt}$$
После того, как определены все функции подстановки (\ref{DefSubsun}), можем выписать уравнение для $\theta$, которое теперь будет иметь следующий вид: $$\theta_t+ F(\theta)f_n(x) \theta_x=0.\tag{2.21}\label{EqMarkSGn}$$
2.3. Построение и анализ решений со сферической симметрией
Построение решений в случае цилиндрической и сферической симметрий опирается теперь на решениях квазилинейного уравнения первого порядка (\ref{EqMarkSGn}). Это уравнение отличается от уравнения (\ref{EqMarkSG0}) тем, что не содержит в записи коэффициентов при производной по $х$ зависимости от $t$. Это упрощает задачу интегрирования этого уравнения. Как можно видеть, это уравнение приводится к уравнению простой волны с помощью замены координаты $x\to \xi$: $$d z_n= \frac{dx}{f_n(x)},$$ откуда находим: $$z_n(x)=\left\{\begin{eqnarray*}&&\frac{1}{\sqrt{2}}\int\frac{dx}{\sqrt{a-x}},\quad n=0,\\&&\frac{1}{\sqrt{2}}\int\frac{dx}{\sqrt{\ln(a/x)}},\quad n=1,\\&&\frac{1}{\sqrt{2}}\int\frac{dx}{\sqrt{a^{-1}+x^{-1}}},\quad n=2\end{eqnarray*}\right.$$ или $$z_n(x) = \left\{\begin{eqnarray*}&&-\frac{1}{\sqrt{2}}\sqrt{a-x},\quad n=0,\\&&-a\sqrt{2}\int\limits^{x}e^{-y^2}dy+z_0,\quad n=1,\\&&\frac{\sqrt{a}}{2\sqrt{2}}\Big(-a\ln\left(x+\sqrt{x^2+ax}+a/2\right)+2\sqrt{x^2+ax}\Big),\quad n=2.\end{eqnarray*}\right.$$ В этом случае, уравнение для $\theta$ примет вид уравнения Хопфа: $$\theta_t+F(\theta)\theta_{z_n}=0,\tag{2.22}\label{EqHophn}$$ которое имеет интеграл движения: $$\theta = H\Big(z_n(x)-F(\theta)t\Big).\tag{2.23}\label{SolmarkSGn}$$ Распределение поля скорости $u$ (\ref{DefSubsun}) имеет теперь вид: $$u(x,t) = f_n(x)F(\theta).\tag{2.24}\label{SoluSGn}$$
Распределение массы вычисляется из соотношения: $$\rho = \frac{\theta_x}{x^n}=\frac{z'_n(x)}{x^n}\frac{H'(\xi)}{1+H'(\xi)F'(\theta)t}.\tag{2.25}\label{DefrhoSGn}$$ Здесь $\xi=z_n(x)-F(\theta)t$. Расчет массы в пространстве производится теперь с помощью следующих соотношений: $$M_{x_1,x_2}= 2^{n}\pi\int\limits_{x_1}^{x_2} \rho(x) x^n dx= 2^{n}\pi\int\limits_{x_1}^{x_2} \theta_x(x) dx=2^{n}\pi\Big(\theta(x_2,t)-\theta(x_1,t)\Big).\tag{2.26}\label{DefMSGn}$$ Отсюда следует, что и в двумерном, и трехмерном варианте модели, масса, содержащаяся в интервале радиальных координат, определяется разностью значений маркеров.
Начальное распределение маркера связано с функцией $H(\xi)$, которая вычисляется из соотношения: $$\theta(x,0)=H(z_n(x)).\tag{2.27}\label{DefBeggt}$$ Соответственно, начальное распределение плотности массы и скорости можно вычислить из соотношений: $$\rho(x,0)=\frac{z'_n(x)}{x^n}H'(z_n(x)),\ \ u(x,0)= f_n(x)F\Big(H(z_n(x))\Big).\tag{2.28}\label{DefBegrho}$$ Поскольку функция $F(\theta)$ является фиксированной, то данное решение не является полным, поскольку начальное распределение скорости задается начальным распределением массы. Как получить общее решение, выясним далее, а здесь рассмотрим пример решения задачи о динамике пыли и образовании сингулярности в распределении массы. Такая задача важна для астрофизики (см. [GZ95UFN] и библиографию там).
Случай плоского фронта $n=0$ допускает вещественное решение лишь на полупрямой при $x\le a$. Это предполагает очень специфическую постановку физической задачи с наличием некоторого барьера в пространстве, за который пыль не проникает. Анализ такой, достаточно экзотической задачи, здесь опустим и далее будем анализировать случаи $n=1,2$.
Поскольку случай сферической симметрии играет в астрофизике более важную роль, рассмотрим примеры решения задачи именно для случая $n=2$. В качестве примера рассмотрим функцию $H(\xi)$ в (\ref{SolmarkSGn}) следующего вида: $$H(\xi)=\rho_0{\rm arctg}\Big(\xi^6/k\Big),$$ где $k$ и $\rho_0$ - постоянные параметры. В начальный момент времени для случая $a=\infty,\ \rho_0=2,\ k=2$ имеем: $$z_2(x)=2\sqrt{2}\sqrt{x},~~z_2(x)=\sqrt{2}/\sqrt{x},$$ $$\theta(x,0)=2{\rm arctg}\Big(z^6_0(x)\Big)=2{\rm arctg}\Big(256 x^3\Big),$$ $$\rho(x,0) = 1536/(65536 x^2 +1),$$ $$u(x,0) = -\frac{2}{\sqrt{x}}\Big({\rm arctg}\Big(256 x^3\Big)\Big)^{1/2}.$$ Выбор начального распределения маркеров в таком виде необходим для того, чтобы распределение плотности в начале координат в начальный момент времени не имело сингулярности. Скорость потока в начальный момент времени в начале координат и при $x\to\infty$ равна нулю. Графики эволюции профилей распределения плотности и скорости потока представлены на рис. (\ref{Pic3}).
- Войдите на сайт для отправки комментариев
- 4147 просмотров
