В ДАННОЙ РАБОТЕ СОДЕРЖИТСЯ ОШИБКА, ПРИВОДЯЩАЯ К ОБРАТНОМУ РЕЗУЛЬТАТУ. МЕТОДОЛОГИЧЕСКИ ВСЕ ВЕРНО, НО ГДЕ-ТО ПОТЕРЯН ЗНАК.
В ИТОГЕ, ПРАВИЛЬНО СЧИТАТЬ, ЧТО ПРИЛИВЫ УВЕЛИЧИВАЮТ НАКЛОН ЗЕМНОЙ ОСИ К ПЛОСКОСТИ ЭКЛИПТИКИ (А НЕ К НОРМАЛИ)
Рассмотрим систему координат ONKz, подвижную, как в Земле, так и в инерциальном пространстве. Уравнения движения Земли под действием момента сил со стороны Луны в этой системе можно найти в работе [1].
$\\A\ddot\theta+[C(\dot\varphi+\dot\psi\cos\theta)-A\dot\psi\cos\theta]\dot\psi\sin\theta=M_N\\A\ddot\psi\sin\theta+2A\dot\psi\dot\theta\cos\theta-C\dot\theta(\dot\varphi+\dot\psi\cos\theta)=M_K\\C(\ddot\varphi+\ddot\psi\cos\theta-\dot\psi\dot\theta\sin\theta)=M_z$ (1)
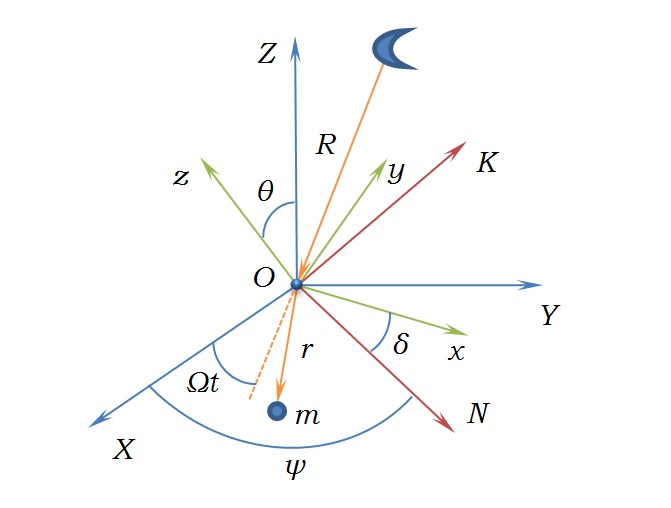 Рис. 1
Рис. 1
Угловая скорость осевого вращения Земли существенно больше угловых скоростей прецессии и нутации, поэтому уравнения (1) можно упростить, отбросив часть слагаемых. Введем обозначение:
$\omega=\dot\varphi+\dot\psi\cos\theta$ (2)
и получим следующую «укороченную» систему уравнений:
$\\C\omega\dot\psi\sin\theta = M_N \\C\omega\dot\theta = -M_K \\C\dot\omega = M_z$ (3)
Момент, действующий на Землю со стороны Луны, может быть представлен как сумма двух моментов, опрокидывающего и приливного. Опрокидывающий момент возникает, благодаря экваториальным вздутиям Земли, а приливный появляется при сносе приливных горбов суточным вращением Земли.
В работе [2] показано, что опрокидывающий момент от Луны равен:
$\boldsymbol{M_1}=\frac{3\mu}{R^3}{\boldsymbol{\alpha}\times(\boldsymbol{J}\cdot \boldsymbol{\alpha})}$ (4)
где $\boldsymbol{J}$ – тензор инерции Земли,
И зависит от направления вектора $\boldsymbol{R}$, соединяющего центры Луны и Земли, в системе ONKz.
Связь между системами OXYZ и NKz осуществляется матрицей поворота $\boldsymbol{A}$, компоненты которой равны:
$\\a_{11}=\cos\psi \\a_{12}= - \sin\psi \cos\theta \\a_{13} =\sin\psi \sin\theta \\a_{21}=\sin\psi\\a_{22} =\cos\psi \cos\theta \\a_{23}= - \cos\psi \sin\theta \\a_{31}= 0 \\a_{32} =\sin\theta \\a_{33}= \cos\theta$ (5)
Раскрывая (4) получим:
$\\M_N=\frac{3\mu}{R^3}(C-A)a_{12}a_{13}\\M_K=\frac{3\mu}{R^3}(A-C)a_{11}a_{13}\\M_z=0$ (6)
При расчете направляющих косинусов следует иметь ввиду, что координаты Луны в инерциальном пространстве изменяются со временем, т.е. угол прецессии Луны меняется по закону:
$ \psi_m=\psi-\Omega t$,
где $\Omega$ – угловая скорость орбитального движения Луны, которая считается постоянной,
$\psi$ – текущее значение угла прецессии Земли, или угловое расстояние линии узлов ON от оси OХ в инерциальном пространстве (Рис.1).
Таким образом, мы получим :
$\\M_{1N}=-\frac{3\mu}{R^3}(C-A)\sin^2(\psi-\Omega t)\sin\theta\cos\theta\\M_{1K}= -\frac{3\mu}{R^3}(C-A)\cos(\psi-\Omega t)\sin(\psi-\Omega t)\sin\theta\\M_{1z}=0$ (7)
При осреднении $M_{1K}$ обращается в ноль.
Среднее значение компоненты $M_{1N}$ соответственно равно:
$\\\overline{M_{1N}}=-\frac{3\mu}{2R^3}(C-A)\sin\theta\cos\theta$ (8)
Перейдем теперь к расчету приливного момента.
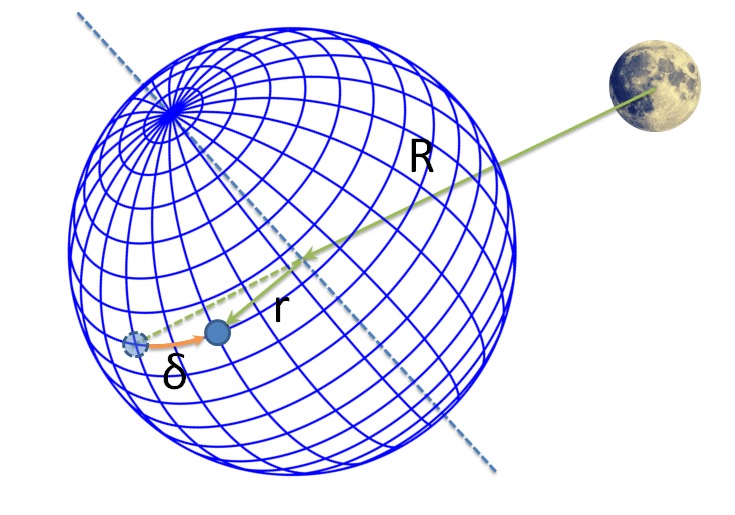 Рис 2.
Рис 2.
Приливный горб, образующийся в подлунной точке, сносится суточным движением Земли на угол $\delta$ (Рис.2). То же происходит и с приливным горбом на противоположной стороне Земли. Расстояния от Луны до приливных горбов равны соответственно:
$\\\boldsymbol{\rho_1}=\boldsymbol{R}-\boldsymbol{r} \\ \boldsymbol{\rho_2}=\boldsymbol{R}+\boldsymbol{r}$ (9)
Момент от ближайшего к Луне горба равен:
$\boldsymbol {M_n}= -\frac{\mu m}{\rho_1^3} (\boldsymbol{-r}) \times (\boldsymbol{R}-\boldsymbol{r})$ (10)
где $\mu$ – гравитационный параметр Луны, $m$ - точечная масса, сосредоточенная в вершине приливного горба, создающая момент равный реально действующему.
Момент от дальнего горба равен:
$\boldsymbol {M_f}= -\frac{\mu m}{\rho_2^3} (\boldsymbol{r}) \times (\boldsymbol{R}+\boldsymbol{r})$ (11)
Результирующий момент равен сумме этих двух моментов. Вспоминая, что векторное произведение вектора самого на себя равно нулю, получим:
$\boldsymbol {M_2}= \mu m \left( \frac{1}{\rho_1^3} -\frac{1}{\rho_2^3}\right ) (\boldsymbol{r} \times \boldsymbol{R})$ (12)
Выразим расстояния до приливных горбов через радиус Земли и расстояние между центрами Земли и Луны, пренебрегая квадратом отношения $r/R$:
$\\\frac{1}{\rho_1^3} =\frac{1}{R^3} \left(1+\frac{3\boldsymbol{R}\boldsymbol{r}}{R^2} \right )\\\frac{1}{\rho_2^3} =\frac{1}{R^3} \left(1-\frac{3\boldsymbol{R}\boldsymbol{r}}{R^2} \right )$ (13)
Разность обратных кубов расстояний равна:
$\frac{1}{\rho_1^3}-\frac{1}{\rho_2^3}=\frac{6\boldsymbol{R}\boldsymbol{r}}{R^5}$ (14)
Таким образом, вектор приливного момента равен:
$\boldsymbol{M_2}=\frac{6\mu m}{R^5} (\boldsymbol{r}\cdot\boldsymbol{R})(\boldsymbol{r}\times\boldsymbol{R})$ (15)
Радиус вектор приливного горба смещен относительно вектора, соединяющего центры Земли и Луны на угол $\delta$. Следовательно, модуль вектора приливного момента равен:
$M_2=\frac{3\mu m r^2\sin2\delta}{R^3}$ (16)
Направление вектора приливного момента определяется векторным произведением $\boldsymbol{r}\times\boldsymbol{R}$. Найдем его компоненты.
Введем матрицу поворота приливного горба:
$\Delta=\begin{pmatrix}\cos\delta &-\sin\delta &0 \\ \sin\delta& \cos\delta & 0\\ 0&0 &1\end{pmatrix}$ (17)
С ее помощью мы получим радиус-вектор дальнего от Луны приливного горба в системе координат ONKz:
$\begin{pmatrix}r_N\\ r_K\\ r_z\end{pmatrix}=\Delta A^{-1}\begin{pmatrix}r\cos\Omega t\\ r\sin\Omega t\\ 0\end{pmatrix}$ (18)
Запишем вектор, соединяющий центры Земли и Луны в системе ONKz:
$\begin{pmatrix}R_N\\ R_K\\ R_z\end{pmatrix}=A^{-1}\begin{pmatrix}R\cos\Omega t\\ R\sin\Omega t\\ 0\end{pmatrix}$ (19)
Скалярное произведение этих векторов равно:
$\boldsymbol{r}\boldsymbol{R}=rR\left(\cos\delta+(1-\cos\delta)a_{13}^{'2}\right)$ (20)
где $a_{13}^{'2}=\sin(\psi-\Omega t)\sin\theta$
Теперь распишем векторное произведение тех же векторов. Так, например, компонента z этого векторного произведения равна:
$(\boldsymbol{r}\times\boldsymbol{R})_z=Ra_{12}^{'}(ra_{11}^{'}\cos\delta-ra_{12}^{'}\sin\delta)-Ra_{11}^{'}(ra_{11}^{'}\sin\delta+ra_{12}^{'}\cos\delta)$ (21)
где штрихи у направляющих косинусов означают, что угол прецессии $\psi$ уменьшен на величину $\Omega t$
Аналогично найдем и другие компоненты.
Введем для краткости вектор:
$\boldsymbol{V}=(\boldsymbol{r}\cdot\boldsymbol{R})(\boldsymbol{r}\times\boldsymbol{R})$ (22)
Его компоненты в системе ONKz мы получим, тщательно перемножив все синусы и косинусы. Так, например,
$V_N=r^2R^2(a_{11}^{'}a_{13}^{'}\sin\delta\cos\delta- a_{12}^{'}a_{13}^{'}(1-\cos\delta)\cos\delta+a_{11}^{'}a_{13}^{'3}(1-\cos\delta)\sin\delta-a_{12}^{'}a_{13}^{'3}(1-\cos\delta)^2)$ (23)
Нетрудно показать, что первое слагаемое в скобках существенно больше всех остальных, поэтому остальными можно пренебречь. Заметим также, что по свойству направляющих косинусов:
$a_{11}^{'2}+a_{12}^{'2}=1-a_{13}^{'2}$ (24)
Таким образом,
$\begin{pmatrix}V_N\\V_K\\ V_z\end{pmatrix}=r^2R^2\sin\delta\cos\delta\begin{pmatrix}a_{11}^{'}a_{13}^{'}\\a_{12}^{'}a_{13}^{'}\\ -(a_{11}^{'2}+a_{12}^{'2})\end{pmatrix}$ (25)
Подставляя значения направляющих косинусов получим компоненты приливного момента в системе ONKz:
$\begin{pmatrix}M_{2N}\\M_{2K}\\ M_{2z}\end{pmatrix}=\frac{3\mu m r^2}{R^3}\sin2\delta\begin{pmatrix}cos(\psi-\Omega t)\sin(\psi-\Omega t)\sin\theta\\-\sin(\psi-\Omega t)^2\cos\theta\sin\theta\\ -sin^2(\psi-\Omega t)cos^2\theta-cos^2(\psi-\Omega t)\end{pmatrix}$ (26)
Очевидно, что среднее значение первой компоненты равно нулю. Зато вторая компонента, отвечающая за угол нутации, при осреднении не исчезает и равна:
$\\\overline{M_{2K}}=-\frac{3\mu m r^2}{2R^3}\sin2\delta\cos\theta\sin\theta $ (27)
Как мы уже выяснили компонента $\overline{M_{1K}}=0$. Следовательно, среднее значение производной угла нутации зависит только от приливного момента и равно:
$\\\overline{\dot\theta}=-\frac{3\mu m r^2}{2C\omega R^3}\sin2\delta\cos\theta\sin\theta$ (28)
Правая часть равенства отрицательна, а это означает, что приливной момент уменьшает наклон земной оси.
_______________________________
Источники информации.
1.Виттенбург Й. Динамика систем твердых тел. Монография. – М.: Мир, 1980.
2. http://www.spacephys.ru/gravitatsionno-prilivnoe-vzaimodeistvie-zemli-i-luny-uvelichivaet-naklon-zemnoi-osi
- Ingus's блог
- Войдите на сайт для отправки комментариев
- 7688 просмотров



Углы Эйлера связывают базис, неподвижный в теле с базисом, неподвижным в инерциальном пространстве. Уравнение моментов может быть записано в проекциях, в одном из базисов. Однако, эти проекции будут связывать декартовы координаты и их производные, а не Эйлеровы углы и их производные, чего хотелось бы. Симметрия тела, у которого осевые экваториальные моменты инерции равны, позволяет выбрать подвижный базис, причем подвижный и относительно тела, и относительно инерциального пространства. Это позволит записать уравнения движения, где искомыми функциями будут Эйлеровы углы.
Уравнения движения получим из теоремы о кинетическом моменте в общей форме.
Абсолютная производная кинетического момента выражается через производную кинетического момента в подвижном базисе следующим образом:
$\frac{\mathrm{d}\boldsymbol{L} }{\mathrm{d} t}=\frac{\partial\boldsymbol{L} }{\partial t}+\boldsymbol{\Omega}\times\boldsymbol{L} $
где $\boldsymbol{L}$ – вектор кинетического момента, $\boldsymbol{\Omega}$ - псевдовектор угловой скорости подвижного базиса.
Обозначим полярный момент инерции тела буквой C, а экваториальные буквой A.
Введем базисные векторы подвижной системы координат ONKz : $\boldsymbol{e_N}$, $\boldsymbol{e_K}$, $\boldsymbol{e_z}$.
Найдем проекции векторов $\boldsymbol{L}$ и $\boldsymbol{\Omega}$ на оси системы ONKz:
$\boldsymbol{L}=A\dot\theta\boldsymbol{e_N}+A\dot\psi\sin\theta\boldsymbol{e_K}+C(\dot\varphi+\dot\psi\cos\theta)\boldsymbol{e_z}$
$\boldsymbol{\Omega}=\dot\theta\boldsymbol{e_N}+\dot\psi\sin\theta\boldsymbol{e_K}+\dot\psi\cos\theta\boldsymbol{e_z}$
Теперь не составит труда найти производную вектора кинетического момента $\frac{\partial\boldsymbol{L} }{\partial t}$ и векторное произведение $\boldsymbol{\Omega}\times\boldsymbol{L}$.
Собрав воедино соответствующие координаты, мы получим базовую систему уравнений:
$\\A\ddot\theta+[C(\dot\varphi+\dot\psi\cos\theta)-A\dot\psi\cos\theta]\dot\psi\sin\theta=M_N\\A\ddot\psi\sin\theta+2A\dot\psi\dot\theta\cos\theta-C\dot\theta(\dot\varphi+\dot\psi\cos\theta)=M_K\\C(\ddot\varphi+\ddot\psi\cos\theta-\dot\psi\dot\theta\sin\theta)=M_z$
где $M_N$, $M_K$, $M_z$ проекции вектора внешнего момента сил на оси системы ONKz.
Поскольку угловая скорость собственного вращения тела (в нашем случае – Земли) существенно больше угловой скорости прецессии и нутации, в базовой системе уравнений можно отбросить слагаемые, содержащие $\ddot\theta$, $\ddot\psi$, $\dot\psi^2$, $\dot\psi\dot\theta$. Вводя обозначение $\omega=\dot\varphi+\dot\psi\cos\theta$, получим «укороченную» систему уравнений:
$\\C\omega\dot\psi\sin\theta = M_N \\C\omega\dot\theta = -M_K \\C\dot\omega = M_z$
Прецессия земной оси не зависит от приливов. А причину приливов вы не указали. Да ее толком никто и не может указать. Так же, как и причину пульсаций Земли и любого вращающегося вокруг своей оси тела
Иван! У меня предложение! Хотелось бы более подробно изложить исходную информацию. Для того, чтобы твоя статья читалась с пониманием, надо бы дать объяснения выбору системы координат. Кроме того, было бы полезно привести вывод исходной системы уравнений. Ты ее выписал, но полезно показать, откуда что берется. Лезть в учебники, на которые ты ссылаешься, у большинства нет возможности и времени. Хорошо бы все такие пробелы восполнить.