Рис. 1.

Приливная эволюция системы Земля-Луна, происходит по причине передачи момента импульса быстро вращающейся Земли орбитальному движению Луны посредством гравитационно-приливного взаимодействия. Приливный горб, деформирующий поверхность Земли оседает не сразу, выходя из подлунной точки, а некоторое время тянет Луну за собой, разгоняя ее на орбите и притормаживая вращение Земли.

Рассчитаем момент импульса системы Земля-Луна (СЗЛ), полагая, что оба тела движутся по круговым орбитам, ось вращения Земли перпендикулярна плоскости ее орбиты. Луне принадлежит часть момента импульса:

$L_m=M_m (R-d)^2 \Omega$,     (1)

где $M_m$ - масса Луны, $R$- расстояние между центрами Земли и Луны, $d$ - расстояние от центра Земли до барицентра СЗЛ, равное

$d=\frac{M_m}{M_m+M_e}R$,     (2)

 $\Omega$ - угловая скорость вращения  СЗЛ вокруг ее барицентра, которая равна

$\Omega=G^{1/2}(M_e+M_m)^{1/2} R^{-3/2}$,     (3)

где $M_e$ - масса Земли, $G$ - гравитационная постоянная.

В итоге, момент импульса Луны в ее движении по орбите равен:

$L_m=k_1 R^{1/2}$,     (4)

где

$k_1=G^{1/2}(M_e+M_m)^{1/2}M_m \frac{M_e^2}{(M_e+M_m)^2}$     (5)

Следовательно

$ \dot{L}_m =\frac{1}{2}k_1R^{-1/2}\dot{R}$     (6)

Поскольку суммарный момент импульса СЗЛ сохраняется, изменение момента импульса Луны зависит от приливного момента, действующего на Землю, взятого с обратным знаком:

$\dot{L}_m=-M$     (7)

В работе [1] было показано, что приливный момент, тормозит вращение Земли:

$M=-\frac{3 G M_m m r^2\sin2\delta}{R^3}$,     (8)

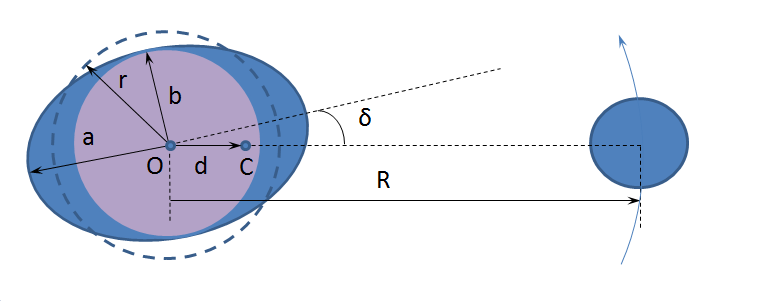
где $m$ - точечная масса, сосредоточенная в вершине приливного горба, создающая момент, равный реально действующему, $r$ - радиус Земли, $ \delta $ - смещение приливного горба относительно подлунной точки.

В результате приливного взаимодействия уровенная поверхность Земли принимает форму эллипсоида вращения[2], полуоси которого равны:

$a=r\left(1+\frac{M_m}{M_e}\frac{r^3}{R^3}\right)$

$b=r\left(1-\frac{M_m}{M_e}\frac{r^3}{2R^3}\right)$     (9)

Результирующий приливный момент определяется массой, находящейся за пределами сферы радиуса $b$. Масса приливного горба, таким образом, равна

$m^*=\frac{1}{2}\rho\Delta V$,     (10)

где $\rho$ - плотность вещества приливного горба, $\Delta V$ - разность объемов приливного эллипсоида и сферы радиуса $b$.

Точечная масса, сосредоточенная в вершине приливного горба, создающая момент, равный реально действующему, очевидно меньше массы всего приливного горба и равна:

$m=m^* k_m$,     (11)

где $k_m <1$ - понижающий коэффициент.

Объем вещества приливных горбов равен

$\Delta V=\frac{4}{3}\pi b^2 (a-b)$     (12)

Величина $\frac{M_m}{M_e}\frac{r^3}{R^3}$ крайне мала, поэтому при вычислении объема $\Delta V$ членами, содержащими данную величину в степени выше первой, можно пренебречь.

Тогда

$\Delta V=2\pi\frac{M_m}{M_e}\frac{r^6}{R^3}$,     (13)

и, соответственно,

$m=\pi\rho\frac{M_m}{M_e}\frac{r^6}{R^3}k_m$     (14)

Введем для краткости обозначения

$k_2=\pi\rho\frac{M_m}{M_e}{r^6}$     (15)

и

$k_3=3G M_m r^2 \sin2\delta$     (16)

Тогда выражение для приливного момента предельно упростится:

$M=-\frac{k_2 k_3 k_m}{R^6}$     (17)

Далее нам следует оценить величину коэффициента $k_m$.

В работе [1] показано, что проекция приливного момента на ось собственного вращения тела в форме эллипсоида равна

$M_z=\frac{3\mu}{R^3}(B_1-A_1)a_{11}a_{12}$,     (18)

где $\mu$- гравитационный параметр возмущающего тела, $B_1$ и $A_1$ - осевые моменты инерции возмущаемого (центрального) тела, принявшего форму эллипсоида вращения в результате приливного взаимодействия, $ a_{11}$ и $ a_{12}$ - направляющие косинусы, определяющие положение радиус вектора, соединяющего центры тел, в системе координат, связанной с центральным телом,

$a_{11}=\cos\psi'$

$a_{12}=-\sin\psi'\cos\theta$     (19)

Не смотря на то, что возмущающее тело обращается вокруг центрального с угловой скоростью $\Omega$, угол прецессии $\psi'=\psi-\Omega t=\delta$ остается неизменным, ведь приливный горб тоже движется, чуть опережая возмущающее тело.

В нашем случае угол наклона оси вращения Земли к плоскости ее орбиты $\theta$ равен нулю.

Следовательно

$M_z=-\frac{3\mu}{2R^3}(B_1-A_1)\sin2\delta$,     (20)

Знак минус в выражении (20) появился, потому что приливный горб опережает подлунную точку и замедляет вращение Земли.

Считая Землю однородным эллипсоидом вращения, запишем ее осевые моменты инерции:

$A_1=\frac{M_e}{5}(b^2+c^2)$

$B_1=\frac{M_e}{5}(a^2+c^2)$     (21)

Тогда

$B_1-A_1=\frac{M_e}{5}(a^2-b^2)$      (22)

Как отмечалось выше, величина $\frac{M_m}{M_e}\frac{r^3}{R^3}$ крайне мала, поэтому при вычислении разности квадратов полуосей эллипсоида вращения мы отбросим слагаемые, содержащие данную величину в степени выше первой и получим, что

$a^2-b^2=3\frac{M_m}{M_e}\frac{r^5}{R^3}$     (23)

и, соответственно,

$M_z=-\frac{9}{10}\frac{ G M_m^2 r^5\sin2\delta}{R^6}$    (24)

Приравнивая выражения (24) и (17) найдем что

$k_m=\frac{9 M_e}{30\pi \rho r^3}$     (25)

Если считать Землю однородным телом со средней плотностью 5500 кг/м3, получим $k_m=0.4$.

В действительности, приливный момент определяется тем веществом, которое находится за пределами сферы радиуса $b$, а его плотность может варьироваться, в зависимости от местности по которой проходит приливный горб – океан или суша. Как показывает опыт, океанские приливные горбы  не следуют строго перед подлунной точкой, поскольку водная оболочка совершенно иначе реагирует на приливные силы Луны, нежели твердая поверхность. Поэтому будем в расчет принимать только твердое вещество поверхности Земли плотностью 2300 кг/м3.

Приравнивая правые части выражений (6) и (17) получим дифференциальное уравнение первого порядка:

$\dot{R}=k_4 R^{-11/2}$      (26)

где $k_4=\frac{2 k_2 k_3 k_m}{k_1}$

Введем параметр $\alpha=\frac{M_m}{M_e}$  - отношение масс Луны и Земли, и выразим коэффициенты $k_1$ - $k_4$ через этот параметр:

$k_1=G^{1/2} M_e^{3/2}\frac{\alpha}{(1+\alpha)^{3/2}}$     (27)

$k_2=\pi r^6 \rho \alpha$     (28)

$k_3=3GM_e \alpha r^2 \sin2\delta $     (29)

$k_4=6 k_m \pi r^8 G^{1/2}Me^{-1/2}\alpha (1+\alpha)^{3/2}\rho\sin2\delta $     (30)

Теперь можно перейти к решению дифференциального уравнения (26).

Допустим, что плотность поверхности Земли равна 2300 кг/м3, а угол смещения приливного горба не зависит от угловой скорости вращения Земли и равен 1°.

Результат расчета представлен на Рис. 2. Шкала времени в миллиардах лет. $R0$ - расстояние от Земли до Луны в наше время.

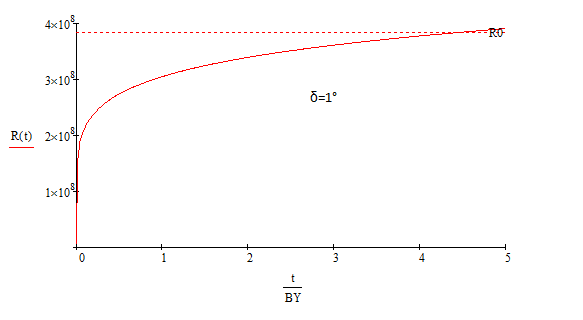Рис. 2.

Таким образом, Луне потребовалось 4.5 миллиарда лет, чтобы с расстояния в один радиус Земли удалиться на 384 400 км.

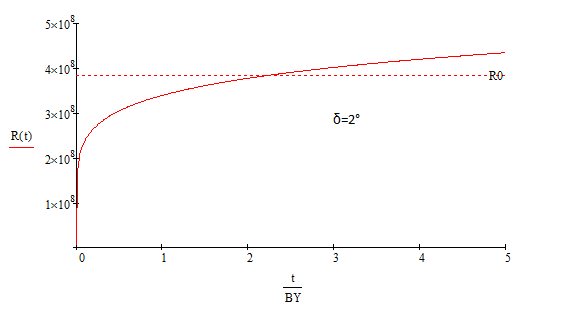 Рис. 3.

 

На самом деле, никто не знает, на какое угловое расстояние смещен приливный горб. Быть может, $\delta=2^{\circ}$. Тогда Луне потребовалось два с небольшим миллиарда лет, чтобы преодолеть известное ныне расстояние (Рис. 3). Согласитесь, что модель слишком чувствительна к плохо поддающемуся оценке параметру $\delta$. Кроме того, смещение приливного горба зависит от угловой скорости вращения Земли. Но это уже другая история.

Рис. 4.

Взглянув на уравнение (26) нетрудно понять, что коэффициент $k_4$ можно найти и иным образом. Скорость удаления Луны в настоящее время известна, как и расстояние до нее. Остается разделить одно на другое и получить:

$k_4=2.086\cdot 10^{38}$  (31)

Подставим это значение в уравнение (26). Теперь оказывается, что Луне потребовалось всего 1.5 млрд. лет, чтобы, отделившись от Земли, добраться до ее сегодняшнего положения (Рис. 4). Парадокс.

Источники информации.

1. http://www.spacephys.ru/gravitatsionno-prilivnoe-vzaimodeistvie-zemli-i-luny-uvelichivaet-naklon-zemnoi-osi
2. http://www.astronet.ru/db/msg/1169697/node25.html