13-01-97067 р_поволжье_а
Наименование: Разработка методов обработки, анализа и визуализации данных в региональных геоинформационных системах с приложениями к задачам экологии и медицины
Предлагаемый проект направлен на решение фундаментальной проблемы разработки математических методов и комплекса программ обработки, анализа и визуализации данных, поступающих и хранящихся в базах данных геоинформационных специализированных систем и систем общего назначения. Основное внимание при разработке создаваемого комплекса обработки данных будет уделено таким разделам геоинформационных баз данных, как экологические и медицинские данные.
В результате выполнения проекта будет разработан комплекс обработки данных, основанный на эффективных известных и новых математических методах и алгоритмах.
| 4.1. Фундаментальная научная проблема, на решение которой направлен проект | |
| Проект направлен на решение фундаментальной проблемы разработки математических методов и алгоритмов обработки, анализа и визуализации данных, содержащихся в базах данных геоинформационных систем различного уровня, с целью их эффективного использования в научных исследованиях в области медицины, экологии и эффективного мониторинга состояния окружающей среды | |
| 4.2. Конкретная фундаментальная задача в рамках проблемы, на решение которой направлен проект (если данная задача является дополнением к теме работ, выполняемых авторами по плану своей организации, - указать название и гос. регистрационный номер этой темы) | |
|
В рамках проекта будут решены следующие задачи: - разработаны новые методы обработки, анализа и визуализации данных, имеющих географическую и территориальную привязку в базах данных геоинформационных систем с использованием изображений Земли из космоса; - будут разработаны специализированные интерфейсы доступа к исходным данным геоинформационных систем и к результатам их обработки с помощью специальных методов визуализации, включающих 3D-модели, анимационные графики и диаграммы; - разработаны специализированные модели в рамках концепции факторов риска развития цереброваскулярной патологии на основе долгосрочного и оперативного сбора информации от медицинских учреждений и состояния окружающей среды, включающей данные экологического мониторинга и данные о магнитном поле Земли |
| 4.4. Ожидаемые в конце 2013 года научные результаты | |
|
К концу первого года работы по проекту получены следующие результаты: - разработан комплекс специализированных алгоритмов обработки данных геоинформационных систем, включающий различные новые и известные методы статистического анализа; - разработан макет интерактивного комплекса программ, совмещающий обработку данных с системой отображения геоинформации и новыми средствами визуализации результатов обработки, в том числе динамических и анимационных диаграмм и графиков; - создана специализированная база медицинских данных в сочетании с синхронными данными о состоянии окружающей среды; - проведены предварительные комплексные исследования региональных медицинских и экологических показателей, в частности, в рамках концепции факторов риска развития цереброваскулярной патологии и других типов паталогий. |
1. Метод условной декомпозиции эмпирических распределений
1.1. Введение
Принцип декомпозиции эмпирических распределений вероятностей (гистограмм) состоит в представлении этого распределения в виде смеси теоретических распределений, каждое из которых отвечает за отдельный физический механизм изменения изучаемого параметра системы. Под смесью понимается формальная сумма отдельных плотностей распределений $\rho_{a}(x|{\bf q}),~a=1,\ldots,M$ физического параметра $x$ с весовыми коэффициентами $p_a$ : $$\rho(x) = \sum\limits_{a=1}^M p_a\rho_a(x|{\bf q}).\tag{1.1}\label{DefSa}$$ Это соотношение можно рассматривать как формулу полной вероятности, в которой параметры $p_a$
- представляют собой априорные вероятности появления признака ${\cal A}_a$ с номером $a$, в системе, а $\rho_a(x|{\bf q})$ - условные вероятности появления значения $x$ изучаемого параметра при условии, что реализуется признак ${\cal A}_a$. Величины ${\bf q}_{a}=\{q_{a1},\ldots,q_{aK}\}$ представляют собой параметры теоретических распределений с номером $a$. Сами признаки ${\cal A}_a$ являются несовместными и отражают реализацию в системе определенного механизма появления значения $x$. Задача декомпозиции состоит в том, чтобы с помощью каких либо вычислений отыскать значения априорных вероятностей $p_{a}$
и всех параметров ${\bf q}_{a}$ теоретических распределений.
Чаще всего причиной, по которой проводится декомпозиция распределений, является многомодовый характер эмпирических гистограмм, выходящий за уровень случайных флуктуаций. Каждая мода (или страта), с точки зрения физики, обычно отвечает за некоторый особый механизм динамики системы. Поэтому выявление свойств отдельных мод позволяет получить некоторые данные об этих механизмах, которые скрыты в шуме случайных флуктуаций. Основной трудностью при реализации декомпозиции является даже не сами математические трудности решения систем уравнений (как правило, нелинейными), а надежная интерпретация самих механизмов формирования отдельных распределений смеси, что является некорректной задачей в смысле явной неоднозначности возможных интерпретаций. На рис. 1 приведен пример гистограммы с двумя модами. Само наличие мод в распределении указывает лишь на существование механизмов, но мало что сообщает о физических условиях их существования. К этой главной трудности добавляются достаточно существенные математические трудности решения систем уравнений для параметров теоретических распределений, что также сопряжено с неоднозначностью решений систем нелинейных алгебраических уравнений для этих параметров, имеющих достаточно большой порядок.
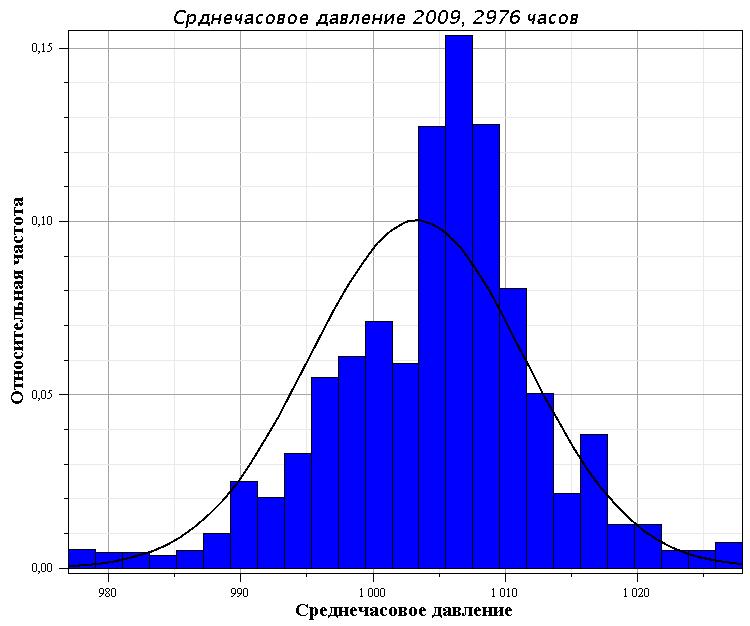
Рис.1. Пример гистограммы распределений, построенной по ряду давления, длиной примерно 2 месяца с шагом 1 час. Сплошной кривой обозначено нормальное распределение со значениями среднего и дисперсии, соответствующих эмпирическим их значениям.
Альтернативой к решению задачи декомпозиции эмпирических распределений в смесь теоретических распределений может служить предлагаемый в данной работе метод условной декомпозиции на смесь других эмпирических распределений. Совокупность эмпирических распределений выделяется из исходного набора данных с помощью некоторой совокупности условий, накладываемых на числовые характеристики исходных рядов наблюдений, которые вычисляются или оцениваются по их значениям. В этом случае проблема интерпретации физических механизмов, соответствующих отдельным распределениям в смеси, если и не решается полностью, то опирается на совокупность исходных условий, которые выбирает сам исследователь. В настоящей работе предлагается простой способ реализации условной декомпозиции распределений на основе эмпирических признаков, проверка возникновения которых строится непосредственно в процессе обработки данных.
1.2. Простая реализация принципа условной декомпозиции
В целом процедура построения декомпозиции исходной гистограммы может быть описана следующим образом. Пусть $x_{i},~~i=1,\ldots,N$ - исходный ряд наблюдений, $X_{i}$ - усредненная его модель, построенная с помощью МНК. Далее, пусть $s_{a},~a=1,\ldots,K-1$ - совокупность границ $K$ интервалов $[s_{a-1},s_{a}],~a=1,\ldots,K$, $s_{K}=max(x_{i},i=1,\cdots,N)$, попадание в которые значений процесса $X_i$ соответствует наступлению события ${\cal A}_{a}$. Это означает, что при выполнении условия:
$$ s_{a-1}\le X_i \le s_{a} \tag{1.2}\label{SCond}$$ значение $x_i$ исходного ряда относится к эмпирическому распределению $\rho_a(x|t)$ и учитывается в соответствующей ему гистограмме. В результате, исходная гистограмма распадается на $K$ отдельных гистограмм, соответствующих условиям \ref{SCond}. Каждая из гистограмм описывает случайные флуктуации в системе при попадании ее в некоторую область усредненных значений наблюдаемых ее параметров.
Рис. 2. Иллюстрация принципа условной декомпозиции на примере временного ряда, обозначенного красной сплошной линией. Синяя кривая -усредненная модель, горизонтальные штриховые линии - границы интервалов. Области значений переменной, относящиеся к отдельным интервалам закрашены соответствующими цветами.
Недостатком такого способа декомпозиции является возможность строить разбиение, основываясь лишь на простых признаках достижения определенных граничных значений самими рассматриваемыми переменными. В реальности, отдельные моды в распределениях могут порождаться разными по сути физическими процессами, различие между которыми нельзя установить, изучая только один вид процесса и, тем более, по пересечениям им некоторых граничных значений. Однако, предлагаемый подход может дать очень полезную информацию в тех случаях, когда диапазоны изменений являются достаточным признаком явления. Примером таких явлений могут служить атмосферные явления, связанные с прохождением над данной территорией областей повышенного давления - антициклоны и пониженного - циклоны.
1.3. Пример декомпозиции распределения значений давления
1.3.1. Общие свойства ряда давления
В качестве примера рассмотрим условную декомпозицию распределения значений давления на одной из метеостанций Ульяновской области за 2009 год. На рис. 3 приведен график изменения давления за 2009 год (сплошная красная кривая) вместе с моделью, построенной с помощью МНК (сплошная синяя кривая). Кроме этого, на графике проведены линии границ, соответствующие области циклонической деятельности (нижняя черная штриховая), анитициклонической (верхняя черная штриховая) и среднее значение за весь период (сплошная черная) .
.jpeg)
Рис.3. Изменение давления за 2009 год (красная сплошная кривая),
модель МНК (синяя сплошная кривая), границы областей (черные штриховые) и среднего значения за весь период (сплошная черная)
На рис. 4 приведена гистограмма распределения давления за всеь 2009 год и нормальное распределение, имеющее среднее и дисперсию, равные среднему и дисперсии самого ряда (сплошная красная кривая).
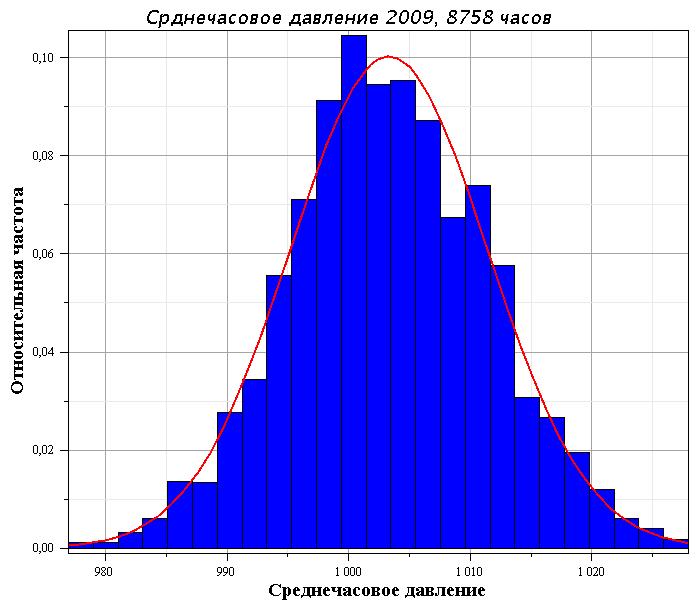
Рис. 4. Гистограмма распределения давления за весь 2009 год, Красная сплошная кривая - нормальное распределение со средним и лисперсией, равной их оценкам по всему ряду.
1.3.2. Модель МНК ряда давления
Модель МНК строится на основе данных о спектральной плотности ряда давления. График спектральной плотности приведен на рис. 5.
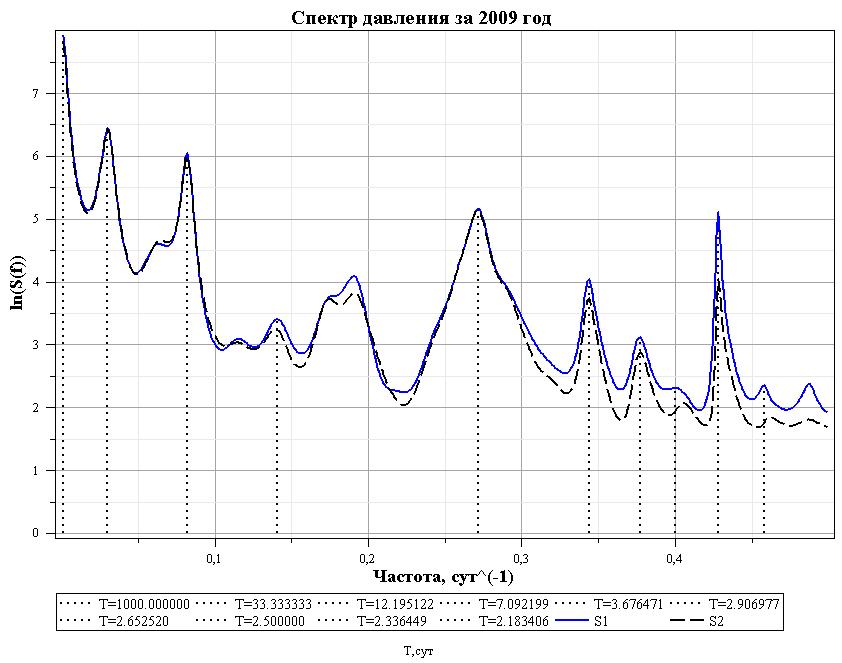
Рис. 5a. График спектральной плотности ряда давления за весь 2009 год. Спектр построен по сглаженному и прореженному ряду косинусным фильтром с окном P=12. После прореживания и векторизации шаг равен 1 сут. Частота Найквиста 0.5 сут${}^{-1}$. Периоды пиков приведены в сутках. Пунктиром изображен автоспектр ряда со сдвигом 12 часов.
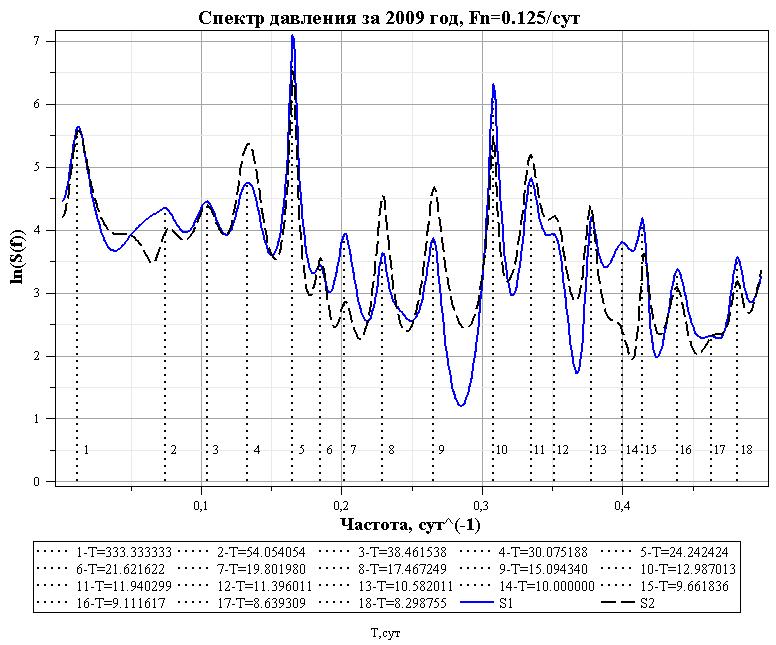
Рис. 5b. График спектральной плотности ряда давления за весь 2009 год. Спектр построен по сглаженному и прореженному ряду косинусным фильтром с окном P=12. После прореживания и векторизации шаг равен 1 сут. Частота Найквиста 0.5 сут${}^{-1}$. Периоды пиков приведены в сутках. Пунктиром изображен автоспектр ряда со сдвигом 2 суток
На рис. 5a видны гармоники соотвествующие периоду $T=33$ сут. (пик 2). Этот пик, а также - пики 3,4, по всей видимости, связанны с лунным приливом. Первый пик, как видно из графика на рис. 5b, является смесью двух близких пиков. Пики 3.4 на рис. 5a являются обертонами лунного прилива.
На рис. 5b видны гармоники соотвествующие периоду $T=333$ сут. Это годовой период, смещенный из-за недостаточности длины ряда. Пики 4 и 5 - это пики связанные с лунным приливом, пик 10 - обертон лунного прилива.
В соответствие со спектром модель МНК строится в форме совокупности 6 основных гармоник в форме модели:
$$P(t)=\sum\limits_{k=0}^{11}A_kF_{k}(t)$$
Здесь $F_0=1,~~F_{2k-1}(t)=\cos(\Omega_k t),~~F_{2k}(t)=\sin(\Omega_k t),~~k=1,\ldots,6$.
Частоты выбраны следующим образом:
$\Omega_1=\pi/3800,~~\Omega_2=\pi/2500,~~\Omega_3=\pi/1488,~~\Omega_4=\pi/744,~~\Omega_5=\pi/288,~~\Omega_6=\pi/144.$
Модель с такими гармониками приведена на рис. 3 синей сплошной линией.
1.3.2. Декомпозиция распределения на отрезке 4 месяца.
Декомпозиция распределения, представленного на рис. 6, строится для следующих границ: $S_1 = \overline{P}-0.26\sigma_p,~~S_2 = \overline{P}+0.26\sigma_p,$ Эти границы приведены на рис. 3 в виде пунктирных линий. Величина $\overline{P}$ представляет собой среднее давление за весь 2009 год. Результаты декомпозиции представлены на рис. 7 a,b,c.
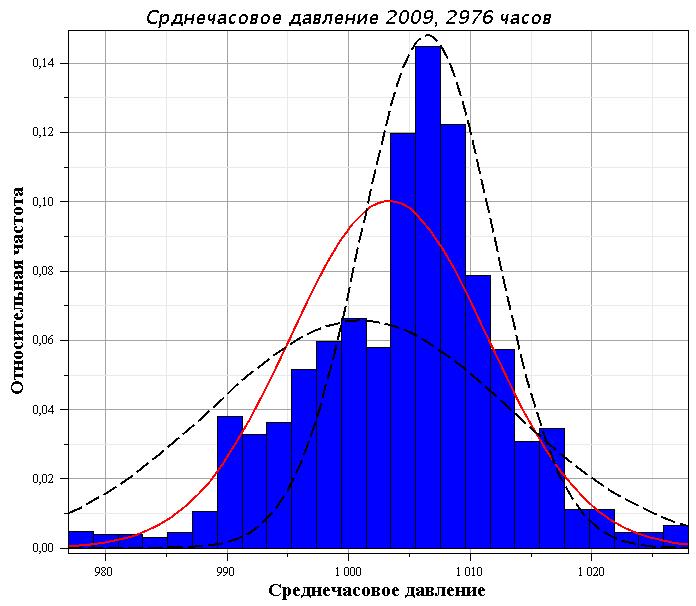
Рис. 6. Распределение давления за первые 4 месяца 2009 года. Красной сплошной линией нанесено нормальное распределение, имеющее среднее и дисперсию исходному ряду. Пунктирами показаны нормальные распределения приближающие моды распределения.
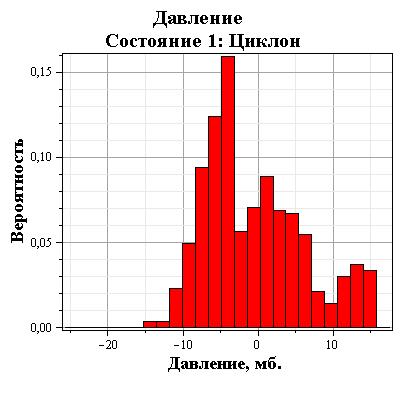
Рис. 7a. Распределение давления за первые 4 месяца 2009 года в диапазоне пониженного давления (циклоническая деятельность). Нулевое значение соответствует среднему давлению за период циклонической деятельности.
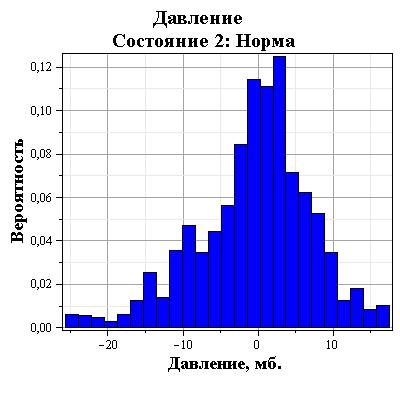
Рис. 7b. Распределение давления за первые 4 месяца 2009 года в диапазоне нормального давления (норма). Нулевое значение соответствует среднему давлению за период номального давления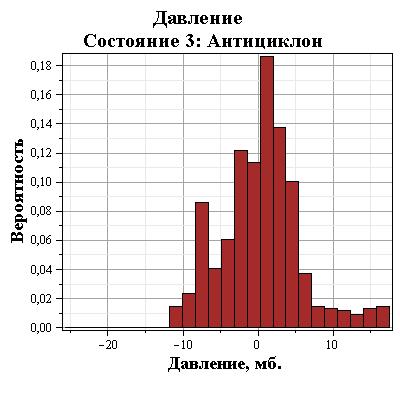
Рис. 7c. Распределение давления за первые 4 месяца 2009 года в диапазоне повышенного давления (антициклоническая деятельность). Нулевое значение соответствует среднему давлению за период антициклонической деятельности.
- Войдите на сайт для отправки комментариев
- 7028 просмотров

.JPG)

