Как известно, Луна удаляется от Земли. Когда это началось, и как долго это будет происходить? И что будет потом? На эти вопросы нет однозначного ответа. Вращательная энергия Земли посредством приливного взаимодействия передается Луне, и та удаляется. Приливное трение «съедает» огромное количество механической энергии, поэтому полная механическая энергия системы Земля-Луна не сохраняется. Однако, выполняется закон сохранения момента импульса. Он не чувствителен к диссипативным процессам!
Представим себе два одинаковых диска, один из которых раскрутили, а потом прижали ко второму. Первый диск будет скользить по второму, постепенно приводя его в движение, но теряя при этом в скорости вращения. В какой-то момент угловые скорости обоих дисков станут равными, и диски будут вращаться как одно целое (Рис. 1).
 Рис. 1
Рис. 1
Закон сохранения механической энергии в данном случае не выполняется, поскольку трение рассеивает часть механической энергии в тепло. Зато выполняется закон сохранения момента импульса, который и позволит нам рассчитать потери энергии и конечную скорость вращения дисков.
В начале, первый диск обладает моментом импульса
$L=I\omega_1$ (1)
и кинетической энергией
$T_1=\frac{1}{2}I\omega_1^2$. (2)
В конце суммарный момент импульса дисков равен
$L=2I\omega$, (3)
а их энергия равна
$T_2=I\omega^2$ (4)
Запишем закон сохранения момента импульса:
$I\omega_1=2I\omega$ (5)
Следовательно,
$\omega=\frac{\omega_1}{2}$. (6)
На трении будет потеряна
$\Delta T=T_1-T_2=\frac{1}{2}I\omega_1^2-\frac{1}{4}I\omega_1^2=\frac{1}{2}T_1$ (7)
ровно половина кинетической энергии первого диска.
Обратимся теперь к системе Земля-Луна. Допустим, что Луна движется по круговой (точнее очень близкой к круговой в любой момент времени) орбите вокруг Земли, и не испытывает никаких гравитационных воздействий, кроме приливного взаимодействия с Землей. Ось вращения Земли о ось орбитального движения Луны совпадают.
В такой модели Луна удаляется от Земли, угловая скорость ее орбитального движения и угловая скорость вращения Земли уменьшаются, пока не станут равными в резонансе 1:1.
Запишем закон сохранения момента импульса для системы Земля-Луна:
$C\omega_0+M r_0^2\omega_1=C\omega+M r^2\omega$, (8)
где $C=8.039\cdot10^{37} $ кг м2 - момент инерции Земли, $\omega_0=7.292\cdot10^{-5}$ - угловая скорость вращения Земли в настоящее время, $M= 7.3477\cdot10^{22}$ кг - масса Луны, $r_0 = 3.844\cdot10^8$ м - среднее расстояние от Земли до Луны в настоящее время, $\omega_1= 2.649\cdot10^{-6}$ рад/с - угловая скорость орбитального движения Луны в настоящее время, $\omega$ - резонансная угловая скорость вращения Земли (и обращения Луны по орбите), $r$ - расстояние Земля-Луна в момент достижения резонанса 1:1.
Разделим левую и правую часть (8) на $ r_0^2 \omega_1 $ и вводя обозначение
$L=\frac{C \omega_0 }{ r_0^2\omega_1}+M$ (9)
получим
$L=\frac{C}{r_0^2}\frac{\omega}{\omega_1}+M\frac{r^2}{r_0^2}\frac{\omega}{\omega_1}$. (10)
Введем новые обозначения
$х=\frac{r}{r_0}$, $y=\frac{\omega}{\omega_1}$ (11)
Согласно третьему закону Кеплера
$\frac{r_0^3}{r^3}=\frac{\omega^2}{\omega_1^2}$ (12)
или, в наших новых обозначениях
$y=x^{-3/2}$ (13)
Подставляя $x$ и $y$ в (10), получим:
$L=\frac{C}{r_0^2} y+M x^2 y$ (14)
или
$L=\frac{C}{r_0^2} x^{-3/2}+M x^{1/2}$ (15)
Это выражение эквивалентно уравнению четвертой степени относительно $x$.
График функции
$f(x)=L-\frac{C}{r_0^2} x^{-3/2}-M x^{1/2}$ (16)
можно видеть на Рис. 2.
.jpg) Рис. 2.
Рис. 2.
Найдем корни уравнения $f(x)=0$ численно:
$x_1=1.44$, $x_2=0.04$
Таким образом, Луна сможет удалиться не более чем на $ 5.532\cdot10^8$ м, что намного меньше сферы действия Земли относительно Солнца ($9.25\cdot10^8$ м).
Сутки при этом станут в 47 раз длиннее, чем сейчас и будут равны лунному месяцу.
Интересно, что резонанс 1:1 возможен с точки зрения математики и на расстоянии в 2.3 земных радиуса, при угловой скорости Земли в 5 раз большей, чем сейчас (т.е. сутки менее 5 часов).
Такая ситуация сомнительна или даже невозможна с точки зрения физики, поскольку Луна была бы разорвана приливными силами, а Земля силами инерции. Другое дело, если Земля и Луна представляли собой тогда аморфные тела – два сгустка материи, вращающиеся как одно целое.
Тот же закон сохранения момента импульса (10) поможет нам заглянуть в прошлое.
Обозначим $\omega_m$ - угловую скорость орбитального движения Луны, а $\omega_e$ - угловую скорость вращения Земли.
По закону сохранения момента импульса:
$\omega_e=\omega_1 r_0^2\left ( \frac{L-M x^{1/2}}{C} \right )$ (17)
По третьему закону Кеплера:
$\omega_m=\omega_1 x^{-3/2}$ (18)
Зависимость этих угловых скоростей показана на Рис. 3.
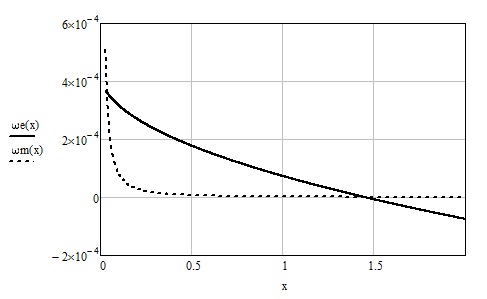 Рис. 3.
Рис. 3.
Глядя, на эти графики, можно подумать, что чудовищные приливные силы довольно быстро отдалили Луну от Земли и сейчас мы наблюдаем угасание процесса ее ухода. Повторюсь, что данная ситуация маловероятна.
Также можно видеть, что после прохождения точки резонанса 1:1 Земля начнет вращаться в обратную сторону. Это тоже маловероятно, поскольку в точке резонанса перестанет действовать механизм передачи момента импульса от Земли к Луне, исчеснет трансверсальная сила от приливных горбов, разгоняющая Луну.
- Ingus's блог
- Войдите на сайт для отправки комментариев
- 6166 просмотров



Уважаемый Ingus! Модель интересная. Но почему не учитывается момент импульса и энергия вращения самой Луны? Тем более, что именно это вращение порождает диссипацию внутри Луны. По этой причине, как считается, Луна повернута к нам одной и той же стороной, что минимизирует приливную диссипацию. По моему, модель надо подправить. А так интересно.
Момент импульса Луны относительно ее оси вращения составляет $1.9\cdot10^{-6}$ суммарного момента импульса системы Земля-Луна. Стоит ли о нем говорить?
Такое значение момента импульса у Луны сейчас. А раньше, когда Луна была ближе? Считается, что Луна раньше находилась гораздо ближе к Земле. Модель твоя должна была бы объяснить удаление Луны с более близкой позиции к современной. Я об этом говорю.
Виктор Михайлович! Спасибо, что обратили внимание. Я как раз над этим думаю. Когда-то Луна вращалась вокруг своей оси ( в какую сторону кстати?). Нужно ввести ее момент в модель, чтобы посмотреть значимость. Сделаю.
Иван! Луна и сейчас вращается, но в резонансе с орбитальным периодом 1:1. Вполне возможно, что система в конце концов должна придти в состояние с резонансом 1:1 и к вращению Земли и Луны одновременно. Луна в этом смысле уникальный случай. Слишком большая масса для спутника. В системах больших планет там резонанс 1:1 встречается не так часто. Примером может служить Ганимед, но это случай как раз обратный твоему. Его влияние на вращение Юпитера незначительно. А вот обратный эффект существенный. С Луной, похоже, что-то подобное. Видимо это надо учитывать Твоя модель нравится своей простотой и наглядностью.
Да. Согласен. Не вышел я еще на нужный уровень( Конечно, следовало бы сказать "Раньше Луна вращалась с большей угловой скоростью"
Найдем корни уравнения $f(x)=0$ численно:
$x_1=1.44$, $x_2=0.04$
Таким образом, Луна сможет удалиться не более чем на $ 5.532\cdot10^8$ м, что намного меньше сферы действия Земли относительно Солнца ($9.25\cdot10^8$ м).
Сутки при этом станут в 47 раз длиннее, чем сейчас и будут равны лунному месяцу.
Интересно, что резонанс 1:1 возможен с точки зрения математики и на расстоянии в 2.3 земных радиуса, при угловой скорости Земли в 5 раз большей, чем сейчас (т.е. сутки менее 5 часов).
Такая ситуация сомнительна или даже невозможна с точки зрения физики, поскольку Луна была бы разорвана приливными силами, а Земля силами инерции.
Уважаемый Ingus, если, всё-таки, абстрагироваться от возможности разрывов Земли и Луны, насколько устойчиво было состояние $x_2=0.04$ и насколько устойчиво будет состояние $x_1=1.44$? Могло ли что-то (например, удар другого космического тела) заставить "путешествовать" Луну в сторону сближения с Землёй от $x_2=0.04$? И сможет ли что-то аналогичное заставить её путешествовать дальше после $x_1=1.44$?
Устойчиво по Ляпунову или по Арнольду?:)
Я работаю над этим. Пока не могу сказать.
Написано:
...где $C=8.039\cdot10^{37} $ кг м2 - момент инерции Земли, $7.292\cdot10^{-5}$ - угловая скорость вращения Земли в настоящее время, ...
Правильно:
...где $C=8.039\cdot10^{37} $ кг м2 - момент инерции Земли, $\omega_0=7.292\cdot10^{-5}$ - угловая скорость вращения Земли в настоящее время, ...
(пропущено $\omega_0=$)
Спасибо! Исправил.
На трении будет потеряна
$\Delta T=T_1-T_2=\frac{1}{2}I\omega_1^2-\frac{1}{4}I\omega_1^2=\frac{1}{2}T_1$ (7)
ровно половина кинетической энергии первого диска.
Интересно! Исходя из общих законов, мы можем в этой ситуации точно рассчитать диссипативные потери, независимо от того - как бы мы ни изощрялись в устройстве идеального механизма сцепления двух дисков.
Приливное трение «съедает» огромное количество механической энергии, поэтому полная механическая энергия системы Земля-Луна не сохраняется. Однако, выполняется закон сохранения момента импульса. Он не чувствителен к диссипативным процессам!
Интересный вывод! Хотя, диссипативные процессы приводят к "деградации" (хаотизации, распределению по хаотическим степеням свободы составляющих систему частиц) не только энергии системы, но и его момента импульса и самого импульса, но "деградацию" энергии системы мы можем зарегистрировать по убыванию внешней энергии системы (в связи с переходом её во внутреннюю), а вот "деградацию" импульса и момента импульса - не можем.
Причина, как я понимаю, заключается в том, что импульс и момент импульса, в отличие от энергии, имеют векторную природу. Поэтому, распределяясь по внутренним степеням свободы, вследствие случайного характера этого распределения их векторная сумма в среднем остаётся равной нулю. Грубо говоря, на каждый вектор внутреннего импульса (момента импульса) найдётся такой же по размеру, но противонаправленный вектор.
Говорят, что сохранение момента импульса связано с изотропностью нашего пространства относительно поворота, т.е. лагранжиан системы не изменяется при повороте системы координат.
Еще мне кажется, что нет никакой векторной природы, как впрочем кватернионной и тензорной. Есть абстрактые понятия для описания природы - вектора, тензоры, кватернионы.. Кватернион, кстати, используется для описания поворота системы координат в трехмерном пространстве...
Можно подействовать кватернионом на псевдовектор) И ничего не произойдет. Шутка. Момент импульса, между прочим, принято считать не вектором, а псевдовектором...
А что такое вектор внутреннего импульса?
Еще мне кажется, что нет никакой векторной природы, как впрочем кватернионной и тензорной. Есть абстрактые понятия для описания природы - вектора, тензоры, кватернионы.
Да, точнее было бы сказать, что не природа у (момента) импульса (псевдо)векторная, а они обладают свойствами (псевдо)векторности. Именно это и обуславливает применимость для их описания абстрактных математических объектов "вектор" и "псевдовектор".
Момент импульса, между прочим, принято считать не вектором, а псевдовектором...
Да, Вы правы, но это никак не влияет на объяснение Вашего утверждения о том, что "закон сохранения момента импульса ... не чувствителен к диссипативным процессам", поскольку векторы и псевдовекторы отличаются только по поведению при некоторых преобразованиях координат, н не при суммировании. А я говорил именно о суммировании случайно распределённых (псевдо)векторов, дающих в среднем 0. Этим и объясняется, на мой взгляд, Ваше утверждение.
Кстати, а Вы как его объясните?
А что такое вектор внутреннего импульса?
Я так назвал (моменты) импульса отдельных элементов (частиц), слагающих систему (тело), которые те приобретают в процессе диссипации. Аналогично тому, как макроскопическая кинетическая энергия переходит во внутреннюю энергию частиц при диссипации.
Кстати, а Вы как его объясните?
Задумался. Каждый атом левого диска на моем рисунке обладает моментом импульса относительно оси диска. Он хочет передать его такому же атому правого диска. Но не может этого сделать непосредственно. Ему мешают. Получается испорченный телефон. В момент контакта дисков он через некторое время понимает, что надо делиться
деньгамиэнергией, чтобы передать момент, и передает его через соседей, а главное через границу, где происходит проскальзывание, а там сами знаете... надо откатить, чтобы проехать. В итоге, все нагрелирукитела, но момент передали в целости и сохранности. Сколько в одном месте убыло, столько в другом месте прибыло.Я так назвал (моменты) импульса отдельных элементов (частиц), слагающих систему (тело), которые те приобретают в процессе диссипации. Аналогично тому, как макроскопическая кинетическая энергия переходит во внутреннюю энергию частиц при диссипации.
Система состоит не из частиц, а из частей, двух, трех и т.д. тел. Момент импульса передается на макроуровне. Крупным дискретом. Он не видит микроуровненвых молекул. А стружка улетает в тепло микроуровня.