1. Бросаем тело прямо к Солнцу
Если скорость запуска тела (броска) равна 2-ой космической, т.е. параболической, тело не упадет обратно на землю, но и не уйдет по параболе в бесконечность, а, потеряв скорость, преодолевая тяготение Земли, остановится на границе сферы действия Земли относительно Солнца.
В сфере действия Солнца относительно звезд тело по инерции сохранит скорость движения Земли по орбите вокруг Солнца. Орбиты Земли и других тел Солнечной системы – сложные спирали с 6-ю изменяющимися во времени параметрами. Средняя орбитальная скорость Земли 29,765 » 30 км/с (примерно 100000 км/ч). С этой скоростью тело будет двигаться вместе с Землей вокруг Солнца, в первом приближении, по круговой орбите.
.jpg)
Чтобы тело двигалось самостоятельно, его надо запустить с Земли с гиперболической скоростью. Тогда при пересечении границы сферы действия Земли относительно Солнца, оно сохранит остаточную скорость DV. Эта скорость геометрически сложится со скоростью, которую тело сохраняет, двигаясь по инерции вместе с Землей по орбите, поэтому его орбита относительно Солнца будет отличаться от земной. Угловой радиус Солнца, видимый с Земли, всего 0 градусов 16 минут. Чтобы брошенное тело попало на Солнце, угол между направлением на центр Солнца и результирующей скоростей rдолжен быть меньше углового радиуса Солнца (см. рис. 1). Из этого следует, что значение DVдолжно быть равно 6383 км/с!
Для сравнения: значение DV при запусках космических аппаратов по полуэллиптическим орбитам к Марсу составляет всего около 3 км/с, а к Венере ‑ 2,5 км/с. Например, с такой скоростью был запущен космический аппарат MarsPathfinder.
Следовательно, чтобы запустить тело с Земли прямо к Солнцу, потребуется колоссальная энергия.
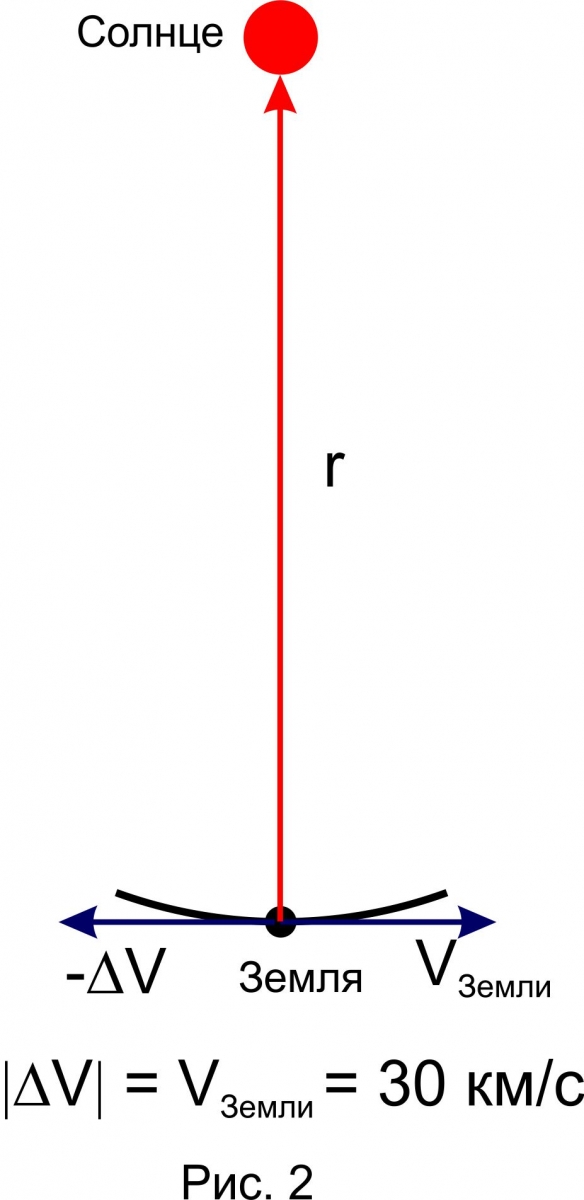
2. Бросаем тело под углом 90° к цели.
Оказывается, в этом случае гораздо легче достичь Солнца. Остаточная скорость DV должна быть равна по абсолютной величине скорости движения Земли по орбите, но направлена в противоположную сторону, чтобы компенсировать скорость, которую тело имеет по инерции вместе с Землей. Тогда оно остановится и само свободно упадет на Солнце (см. рис. 2).
Интересно, что чем дальше планета от Солнца, тем меньше потребуется энергии, чтобы таким способом бросить тело на Солнце. В отличие от твердотельного вращения, при котором скорость возрастает с расстоянием от центра вращения, при кеплеровском вращении скорость падает с расстоянием r от центра вращения (притяжения) по закону обратной пропорциональности корню из r.
3. Бросаем тело в противоположную от Земли точку Солнца
Если векторы DV будут направлены в сторону, противоположную скорости движения Земли по орбите, а по абсолютной величине находиться в пределах 0 < DV< |30|, то, складываясь с вектором скорости движения по инерции, они дадут ряд векторов, направленных в сторону движения Земли (рис. 3). Полученные при этом скорости окажутся меньше круговой относительно Солнца, поэтому орбиты будут представлять собой семейство внутренних эллипсов с афелиями в точке запуска.
Интересно, что движение тела по таким орбитам происходит в сторону, противоположную направлению запуска. (Как хозяин посылает собачку домой, а она все равно бежит за ним). Чем меньше суммарный вектор, тем уже эллипс. Можно подобрать такой суммарный вектор, что движущееся по нему тело попадет на Солнце в точке перигелия орбиты, то есть в точке, противоположной Земле. Значение |DV| такого запуска по абсолютной величине очень мало отличается от орбитальной скорости Земли, но все же меньше ее.
Таким образом, запуск тела на Солнце по 3-му варианту потребует меньше энергии, чем по 2-му и гораздо меньше, чем по 1-му.

- Войдите на сайт для отправки комментариев
- 6424 просмотра



Интересное дополнение сделал fundaev.
А главное вовремя :)
http://spacephys.ru/apparat-messenger-vyshel-na-orbitu-merkuriya
Хотелось бы отметить еще один интересный факт. В случае перелета с Земли на Венеру по эллипсу Гомана (такая траектория характеризуется минимальной характеристической скоростью) при отлете от Земли нужно иметь скорость 2.53 км/с. Для полета на Марс - 2.98 км/с. А для полета на Меркурий - 7.5 км/с(!) Т.е. "свалиться" на Меркурий в 2 с лишним раза труднее, чем "допрыгнуть" до Марса. Не зря к нему летают по траекториям, предусматривающим пертурбационный маневр.
Рахиль Менашевна! Задача интересная! Спасибо! Я вставил уменьшенное изображение из Вашего объяснения в начало для улучшения визуального эффекта.
Очень неожиданный, но математически обоснованный вывод.
Возможно, и снег с крыши можно сбрасывать более рационально? Это актуально в настоящий момент.